
黒木研究室は物性物理学理論の研究室で、物理現象に対してコンピューターや解析的な計算等の理論的な手法で研究しています。 主として以下にあげるテーマを研究対象としています。
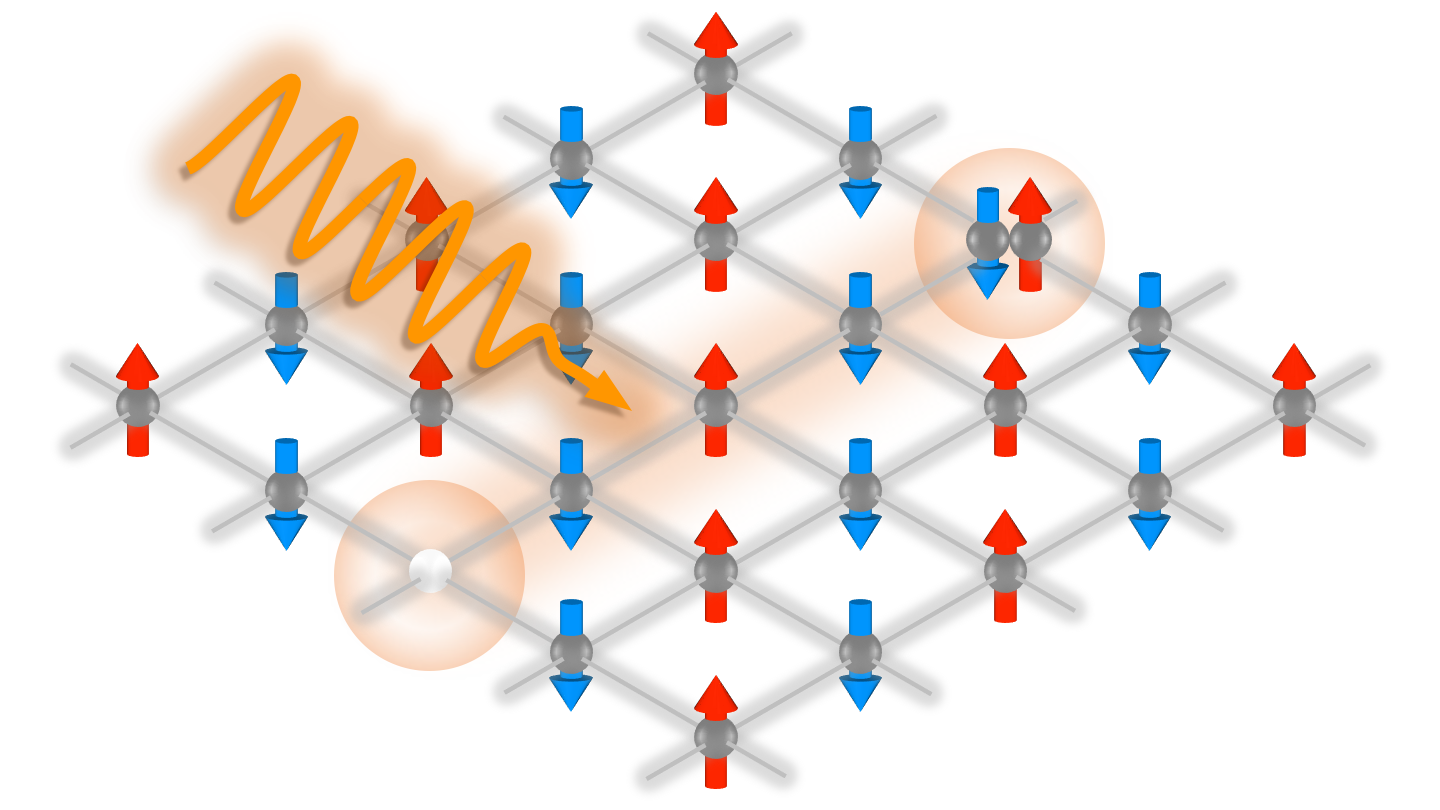
超伝導とは、物質を十分に低温に冷やすと、ある温度(転移温度)以下で電気抵抗がなくなる現象です。1911年に見つかったこの現象は、1950年代にバーディーン、クーパー、シュリーファーによるBCS理論により、理論的解決をみました。ながらく転移温度の世界記録は20K程度の低温でしたが、1986年に見つかった銅酸化物超伝導体は転移温度が130Kを超え、大きなブレークスルーとなりました。このような「高温超伝導」はBCS理論では説明がつかず、世界中の物理学者をひきつけ、強相関電子系における超伝導に関する関心が急速に高まりました。電子と電子との間に働くクーロン反発力(電子間相互作用)の効果が物性に大きな影響を及ぼすと考えられる系は、一般に強相関電子系と呼ばれています。このような強相関電子系に対する研究は磁性等に関係して古くから行われて来ましたが、とりわけ、銅酸化物高温超伝導の発見以来、爆発的な勢いで行われるようになりました。より最近では、2008年に鉄ニクタイド系高温超伝導体が発見され、多軌道系における電子相関と超伝導の研究が進みました。
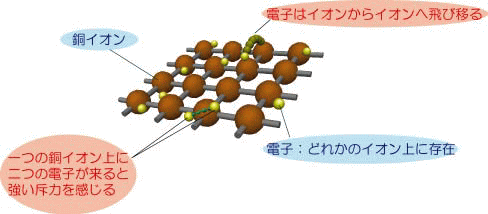
たとえ強相関電子系といえども、物性は電子間相互作用だけで決まるわけではありません。各電子の運動エネルギーの部分も重要な役割を果たします。量子力学によると、電子は「粒子」としての性質と「波」としての性質を持ち、各電子の運動エネルギーは波としての性質を表す波長の逆数(「波数」という)」で決まります。自由な電子の場合、運動エネルギーは波数の2乗に比例しますが、固体中ではこの関係は一般に物質に依存する複雑なものになります。波数と運動エネルギーの関係を「バンド分散」といいます。このバンド分散の構造が物質の性質を決める上で、極めて重要な役割を果たします。バンド構造は結晶構造や軌道(波動関数)の異方性等に大きく依存しています。バンド構造や結晶構造は固体中における電子の活動舞台となります。正しい模型を構築するには正しいバンド構造を考慮する必要があります。実際、例えば鉄ニクタイド系高温超伝導体では鉄の5つのd軌道を起源とするバンドが複雑に絡み合ってフェルミ準位近傍の電子状態を形成しています。このような複雑なバンド構造を多体模型に取り込むことによって、はじめて物性の正しい理解が可能となります。
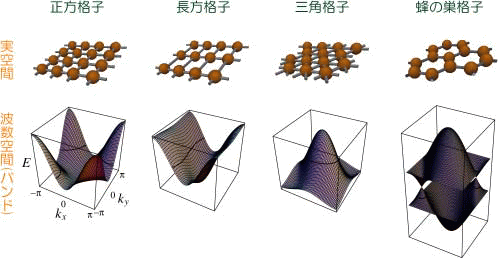
私たちの研究室では固体中の電子の活動舞台であるバンド構造を考慮し、かつ電子間相互作用も考慮した、なるべく簡単化された模型を用いて、超伝導に関する研究を行っています。目標は一つは既存の超伝導体における実験事実を理論的に理解することです。もう一つの目標は、既存の実験事実の理解から得た知見を元に、未知の超伝導体を理論的に予測、予言することです。
熱電効果の一つであるゼーベック効果に関する理論研究を行っています。ゼーベック効果とは、物体に温度の高いところと低いところがあるとき、その温度差に比例した電圧が発生する現象で、その比例係数をゼーベック係数といいます。温度差や熱はいたるところに存在するので、それを効率よく電気に変換できれば、幅広い応用も期待されます。ところが一般にゼーベック係数が大きい物質は半導体に多いため、高い電圧が生じても大きな電流を流すことができず、電力としては大きなものになりません。大きなゼーベック係数と高い電気伝導度が両立した、高い「電力因子」を持つ物質を探索することが重要となります。我々は、高い電力因子を得るためにはどのようなバンド構造が理想的であるかの研究を行い、既存熱電物質における高熱電性能の起源を理解するとともに、新規熱電物質の探索に理論研究を役立てようとしています。
バンド構造とひとくちにいっても、様々な要素がありますが、我々はとくに「バンド形状」という観点に着目しています。ここで「バンド形状」というのは、電子の波数に対してエネルギーがどのように変化するか、ということです。波数空間の特定の領域でバンドがほぼ平坦な分散を持ち、その他の領域では急峻な分散を持つとき、分散が切り替わるエネルギーの付近にフェルミ準位があると、高い電力因子を生み出すことを示しました。温度差によって電気が生じるときには、反対の電荷をもった電子とホールが同じ方向に流れてしまいますが、上記のようなバンド形状の場合は電子とホールの速度に差がつきやすいためです。我々はこのバンド形状を「プリン型」と呼び、さまざまな既存熱電物質の高い性能の解釈に適用してきました。
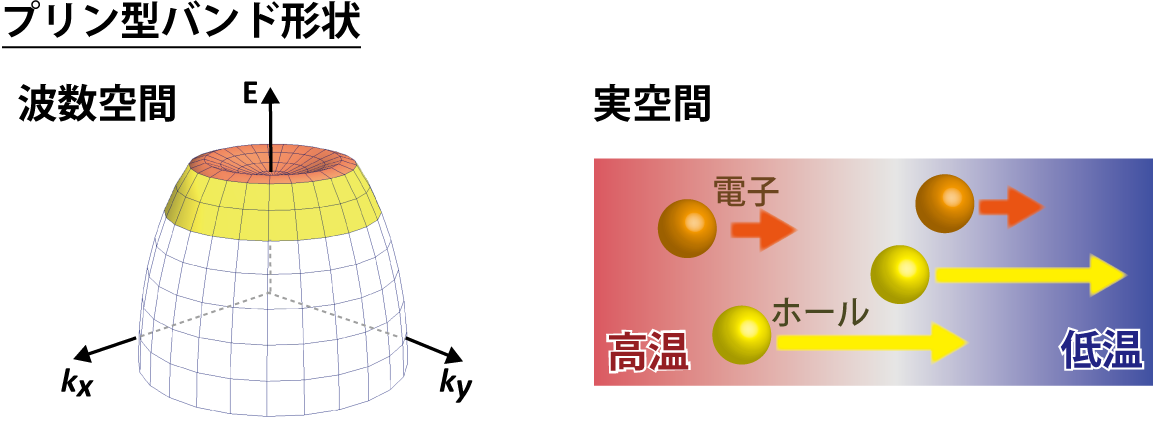
熱電性能を支配するもうひとつの大きな要素は熱伝導です。物体中のある場所と別の場所の間に温度差をつけても、熱伝導がよいとその温度差がすぐに解消されてしまい、高い熱電性能を得るには不利です。物質中で熱を運ぶ担い手には電子とフォノンがいます。電子の熱伝導度と電気伝導度の間には一般にWiedemann-Franz則があり、電力因子を上げるために電気伝導度を大きくしても、電子の熱伝導度も同時に上昇してしまいます。しかし、ある種の状況下ではこの状況が破れることがあり、我々の研究室ではその条件を調べています。電気伝導度の比較的低い物質では、フォノンによる熱伝導を抑制することが重要であり、そのための条件を探索することも重要な研究課題となっています。
乱れた系において、干渉効果によって拡散が抑制される現象をアンダーソン局在といいます。この概念は1958年に、不純物半導体におけるスピン共鳴に関する実験を説明するために、Philip Andersonによって提案されたものです。初期の研究は乱れた固体における電子波動関数の局在に焦点が置かれていましたが、音波や光、冷却原子系での物質波といったあらゆる種類の波について、アンダーソン局在が起こりうることがわかってきました。
乱れを強くすることによって起こる局在-非局在転移が連続的な量子相転移であることが、1980年代はじめに明らかになりました。これは大きなブレイクスルーであり、これにより連続的な熱相転移を理解するために発展したアイディア、特に繰り込み群やそれに関連したスケーリング理論を、このアンダーソン転移に適用できるようになりました。その後、アンダーソン転移における波の強度分布は、マルチフラクタル的であるという、独特かつ美しい側面を持つことが明らかになりました。アンダーソン局在は量子ホール効果においても重要な役割を果たしており、量子ホールプラトー間の転移も一種のアンダーソン転移です。
アンダーソン局在とアンダーソン転移は、解析的に取り扱うのが非常に難しい問題であり、完全に満足のいく包括的な解析的理論は未だ存在しません。我々の研究は、高精度な数値シミュレーションによってこのギャップを埋めることに焦点を置いたものであり、日本やイギリス、ドイツにいる研究者と連携して研究を行っています。特に、対称性や次元性と関連した定性的な問題を明らかにすることや、臨界現象やマルチフラクタル性の定量的な探求に興味があります。これらはアンダーソン局在を定性的また定量的に理解するために役に立っています。

相関電子系の研究はその多くが平衡状態、つまり物質の巨視的な物理量が時間とともに変化しない状態を対象としてきました。しかし、近年の光学技術の発展が、平衡状態から外れた領域へと物質を励起しその高速ダイナミクスを観測可能としたことで、非平衡状態における物性の理解が重要な課題になりました。非平衡状態は物質が固有に持つ電子的性質のプローブや相転移起源の解明にも有用ですが、外場を用いた物質操作による創発物性の舞台としても注目されています。平衡状態にない新たな相を光で導く光誘起相転移が代表的な例で、光によって絶縁体を金属に変えたり、光で超伝導状態をつくり出す研究も進められています。
弱い外場に対して平衡状態からのわずかなズレを調べる手法として線形応答理論がありますが、強い外場によって駆動された系では線形応答理論では扱えない物質の非線形な応答が現れます。非線形応答は物質中で起こる非平衡現象の基礎的な理解にも重要ですが、応用の観点からも精力的に研究が進められています。例えば、空間反転対称性が破れたバルク結晶では光が直流電流を生成する二次の非線形効果があり、この現象は従来のp-n接合を必要としない光起電力効果として太陽電池などへの応用も期待されています。
非平衡・非線形応答領域の物理は量子多体問題としてもチャレンジングな系で、未開拓な研究課題の宝庫です。特に、我々がこれまでに研究してきた相関電子系は平衡状態でも豊かな物性を示してきましたが、開拓領域を非平衡系にまで拡大することでさらに多彩な電子状態や応答現象を見出すことができると期待しています。そのため、我々は数値的な時間発展の手法なども駆使して、相関電子系の未開拓地である非平衡・非線形応答領域に挑戦しています。