
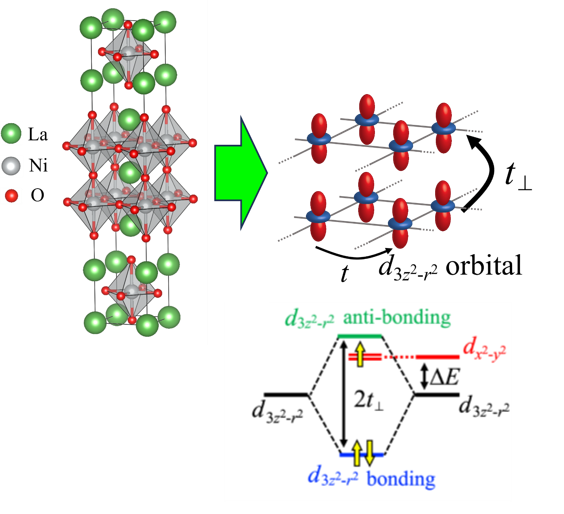
2023年に二層型ニッケル酸化物La3Ni2O7 (図左)が圧力下において最高Tc=80K超の高温超伝導を示すことが発見された。この物質は、2017年に当研究室において行った理論研究において、高温超伝導の可能性が議論されていた物質である[M. Nakata et al., Phys. Rev. B 95, 214509 (2017)]。そこでのポイントは、二層それぞれのニッケルdz2(=d3z2-r2)軌道間の電子のホッピングが大きく、かつ、dz2軌道がほぼハーフフィルド(サイト数=電子数)になることが、超伝導に有利にはたらく(当時はincipient bandという言葉を用いていなかったが、実質的にその効果)ということであった(図右)。当時は予想していなかった圧力下ではあるものの、現実に高温超伝導が実現したことを受けて、圧力下における結晶構造を取り込んだ、dz2軌道とdx2-y2軌道からなる有効模型を構築し、揺らぎ交換近似を用いて、超伝導の解析を行った結果、Tc=80Kと整合する結果を得た[H. Sakakibara et al., Phys. Rev. Lett. 132, 106002 (2024)、プレスリリースはこちら]。
二層型における理論と実験の整合性を受けて、三層型ニッケル酸化物La4Ni3O10の理論研究にも取り組んだ。超伝導がおこるとすれば、二層型と同様、圧力下であるとの仮説に基づき、圧力下の構造を第一原理計算によって決定した。そのうえで、二層型と同様に有効模型を構築して超伝導に関する理論解析を行ったところ、二層型ほど高いTcではないにせよ、incipient bandの効果によって超伝導になる可能性を見出した。そこで、物質材料研究機構の高野義彦氏の実験グループと共同研究を行い、La4Ni3O10が圧力下においてTc =20~30Kの超伝導を示すことを見出した[H. Sakakibara et al., Phys. Rev. B 109, 144511 (2024)]。
上記の解析で用いた揺らぎ交換近似は、強相関効果を近似的にしか取り込めないため、相補的な手法として、密度行列繰り込み群による研究も行った。一次元系という制限はつくものの、相関関数を数値的に厳密に計算できるという強みを活かし、二層型ニッケル酸化物の電子状態を模した二軌道ハバード梯子模型の解析を行った。その結果、dz2軌道の鎖間ペアの相関が発達し、またdx2-y2軌道の鎖間ペアの相関も発達することを見出した[T. Kaneko et al., Phys. Rev. B 109, 045154 (2024)]。 この研究では、軌道間のフント結合の効果を取り込まなかったが、続いて、フント結合の効果を取り込んだ二軌道t-J梯子模型についても密度行列繰り込み群により解析を行った。dz2軌道、dx2-y2鎖間ペアの相関のみならず、一見すると、ペアを形成する引力がないように思える二つの軌道間ペアの相関も発達することを見出した[M. Kakoi et al., Phys. Rev. B 109, L201124 (2024)]。
熱電物質の理論研究において、「どのような電子バンドが望ましいか」あるいは「どのようなフォノン状態が望ましいか」という研究は数多くなされているが、電子とフォノンが互いに散乱する効果については未知のことが多い。我々は、電子フォノン相互作用が、電気伝導性あるいは熱電特性を決めるうえでどのような役割を果たすかを調べた。
我々はまず、層状物質ZrS2およびZrSe2に注目し、電気伝導率に対する電子フォノン散乱効果を、第一原理計算によって調べた。およそ50ケルビン以下ではバレー内の音響フォノン散乱が支配的である一方、ある程度以上の高温になると、バレー内の光学フォノン散乱が支配的になることがわかった。本物質はマルチバレー物質として知られるものの、バレー間の散乱は実は重要ではないことが明らかになった[H. Mori, M. Ochi, and K. Kuroki, Phys. Rev. B 104, 235144 (2021)]。
また、より単純なモデルに立ち返り、フォノンによる電子散乱が熱電性能を増強する可能性を調べた。ナイーブに考えると、散乱の効果は電子寿命を縮めるものであり、良い効果はうまなさそうである。しかし、電子キャリアとホールキャリアの一方のみを強く散乱するような非縮退2バレー系を考えることによって、電子ホール非対称性を強めることがゼーベック係数の増大に繋がることがわかった[M. Ochi, Phys. Rev. B 108, 195139 (2023)]。
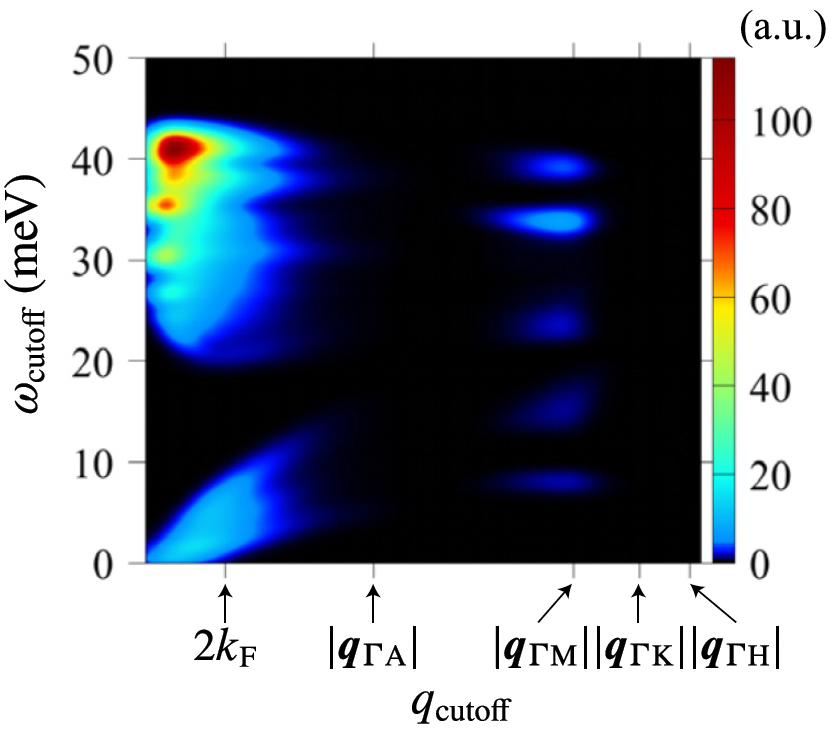
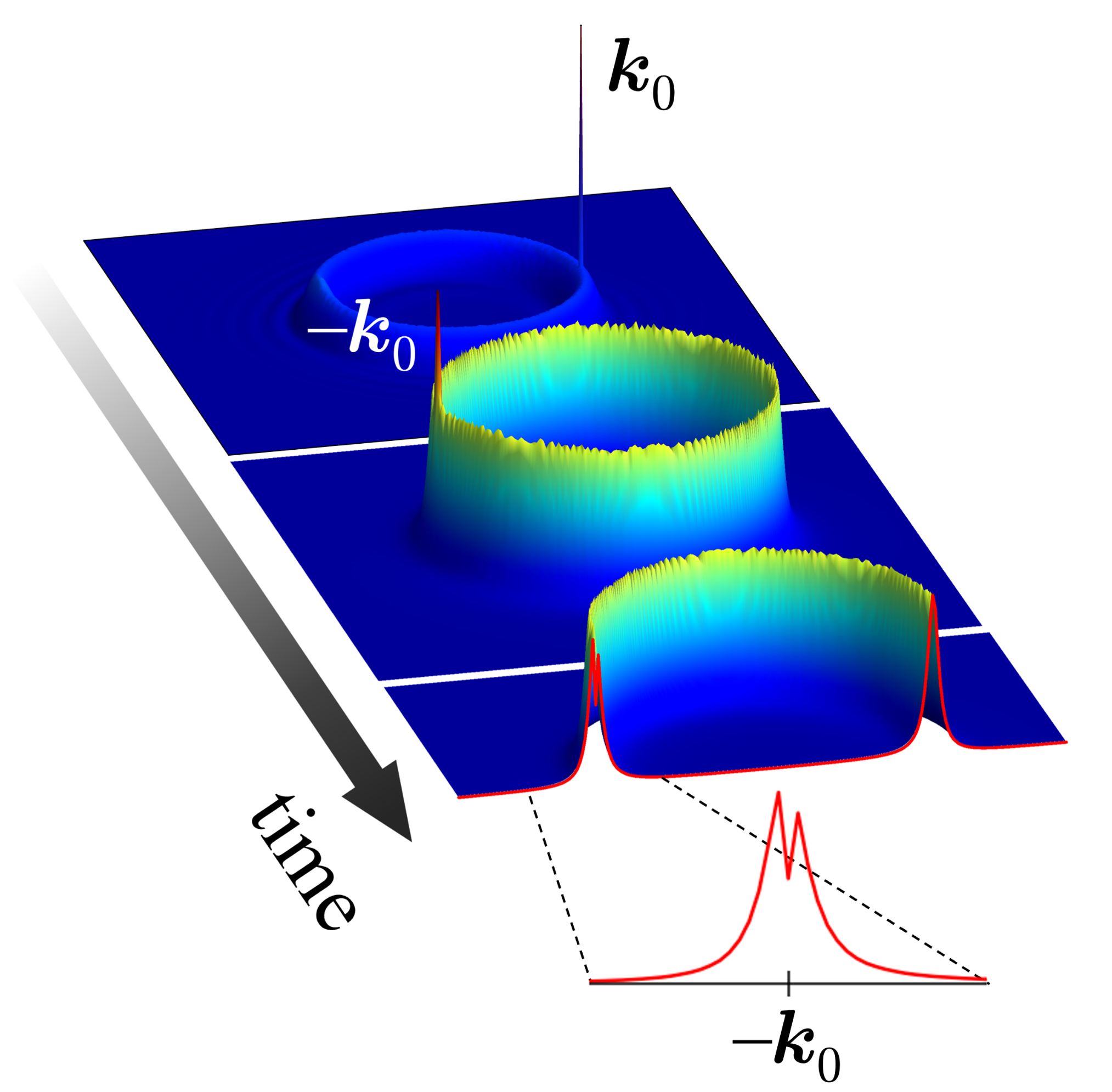
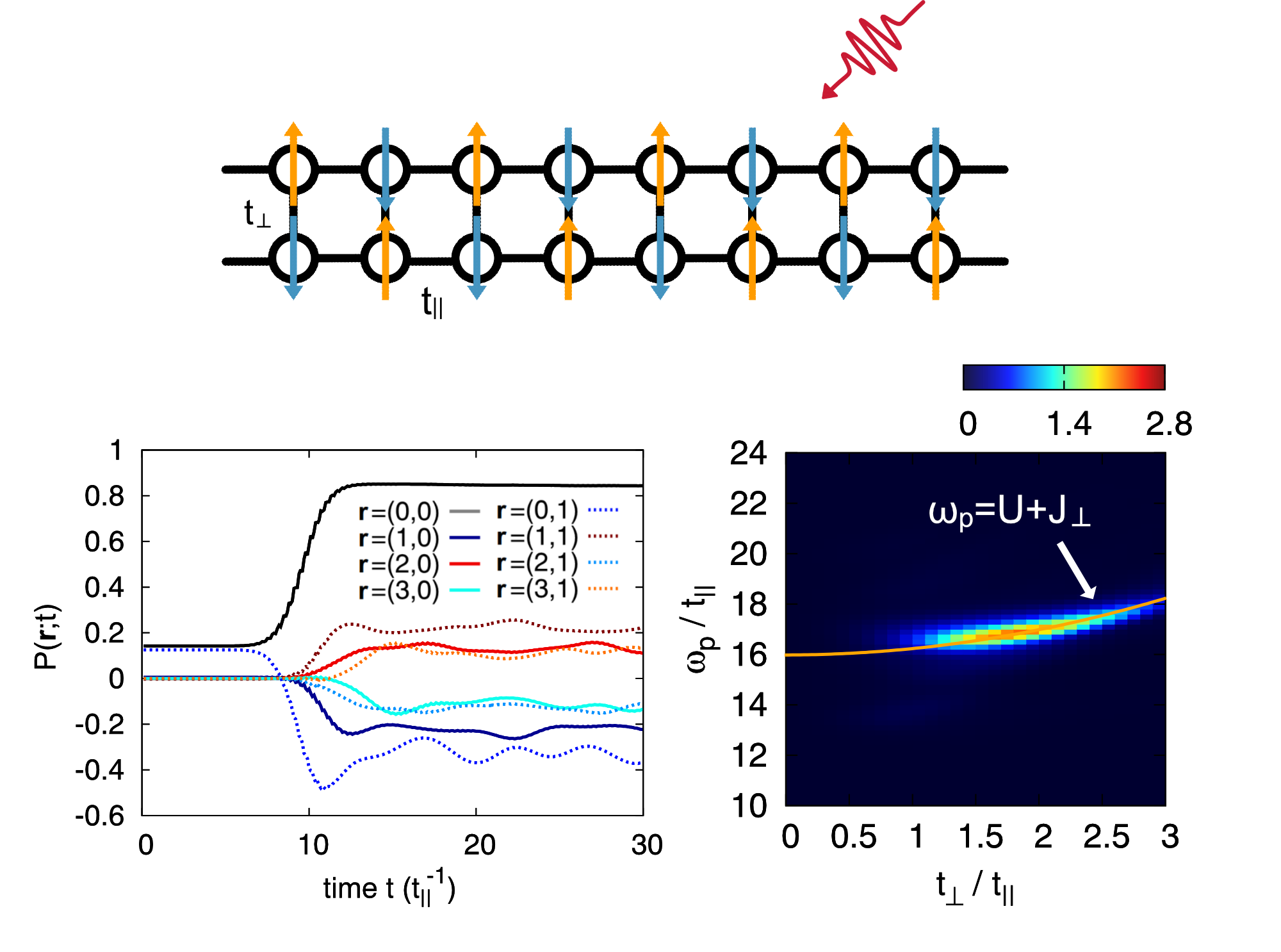
冷却原子気体では、粒子密度の分布を実空間・運動量空間で時間を追って観測できるため、非平衡ダイナミクスを研究するための理想的なプラットフォームとなる。我々はスピン軌道相互作用と無秩序ポテンシャルを用いて、物質波の輸送ダイナミクスを調べた。無秩序な系では一粒子干渉の効果によって、後方散乱が増大されるが、スピン軌道相互作用が存在すると後方散乱はむしろ減少する。我々はこの後方散乱の増大と減少の競合を、運動量分布の時間発展に見出した(図)。さらに、解析計算によって増大から減少へのクロスオーバーの時間スケールを、スピン軌道相互作用の大きさの関数として導出した[M. Kakoi and K. Slevin, Phys. Rev. A 109, 033303 (2024)]。
強い電子間斥力によって生じるモット絶縁体は強相関電子系の典型的な例であるが、モット絶縁体において光で誘起される電子状態とそのダイナミクスの解明は強相関物質の光応答や光制御の理解につながるものである。モット絶縁体の光励起状態にはηペア状態(電子-電子ペアの符号がサイト毎に交替した状態)など平衡系には現れない電子状態が生じ得ることが指摘されている[T. Kaneko et al., Phys. Rev. Lett. 122, 077002 (2019)]。我々は、ηペア状態を含め、光によってキャリアが生成された強相関電子系に現れる電子状態の研究を進めている。
我々は、これまで調べられてきた1次元系からの理論の拡張を目指し、2本鎖から成る梯子構造のハバード模型において相関電子状態の光誘起ダイナミクスについて調べた。厳密対角化法などを用いて、梯子構造においても光照射によってηペア状態が生じることを示し、鎖間の結合の強さおよび照射光の分極方向に依存した梯子系に固有なηペア状態の誘起性を明らかにした。最適な鎖間結合の強さにおいては、従来の1次元鎖よりも大きなηペア相関が生じ得ることもわかった[R. Ueda et al., Phys. Rev. B 109, 075122 (2024)]。
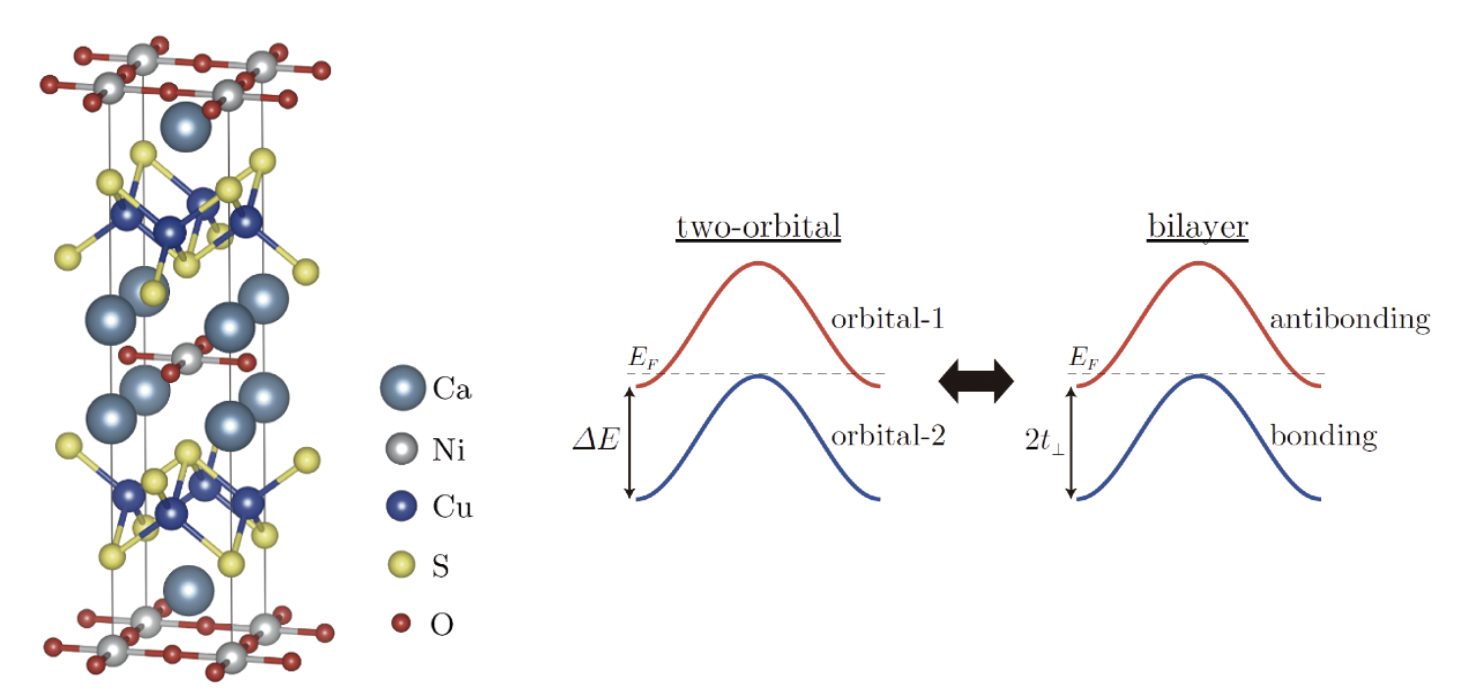
Ba2CuO3+δの研究においては、異なる軌道成分を持つバンド間においてもincipient band 機構が働くことを見出したが、これに触発され、d8 電子配置を持つ複合アニオン化合物AE2NiO2X2 (AE = Sr,Ca; X = Cl,F,H等)において、多軌道型のincipient band機構による高温超伝導がおこる可能性があることを提唱した。多軌道型のincipient band機構においては、軌道間のエネルギー準位の開きが大きいときに超伝導が増強されることが示されるが、これらの物質では、複合アニオンによる結晶場効果によって、dx2-y2軌道とそれ以外のd軌道のエネルギー準位差が大きくなり、dx2-y2以外のバンドがフェルミ準位の直下に潜ったincipient状態にあるとき超伝導に最も有利になることを示した[N. Kitamine et al., Phys. Rev. Res. 2 042032(R) (2020)]。
動的平均場理論は、強相関系を取り扱う手法としてその有用性が示されてきたが、非局所効果を取り込めないため、非従来型異方的超伝導の研究などには直接使うことができない。非局所効果を取り込むためのいくつかの拡張が考案されているが、一般に非常に高い計算コストを必要とし、多バンド・多軌道系のような多自由度系に適用することは困難である。我々のグループはフル・バーテックスの周波数依存性に着目し、非常に低い計算コストで動的平均場理論の計算を行う手法を開発した[R. Mizuno et al., Phys. Rev. B 104, 035160 (2021)]。さらに、この同じ周波数依存性の観点から、非局所性を低コストの計算で取り込む手法を開発し、多自由度系にも適用できることを示した。
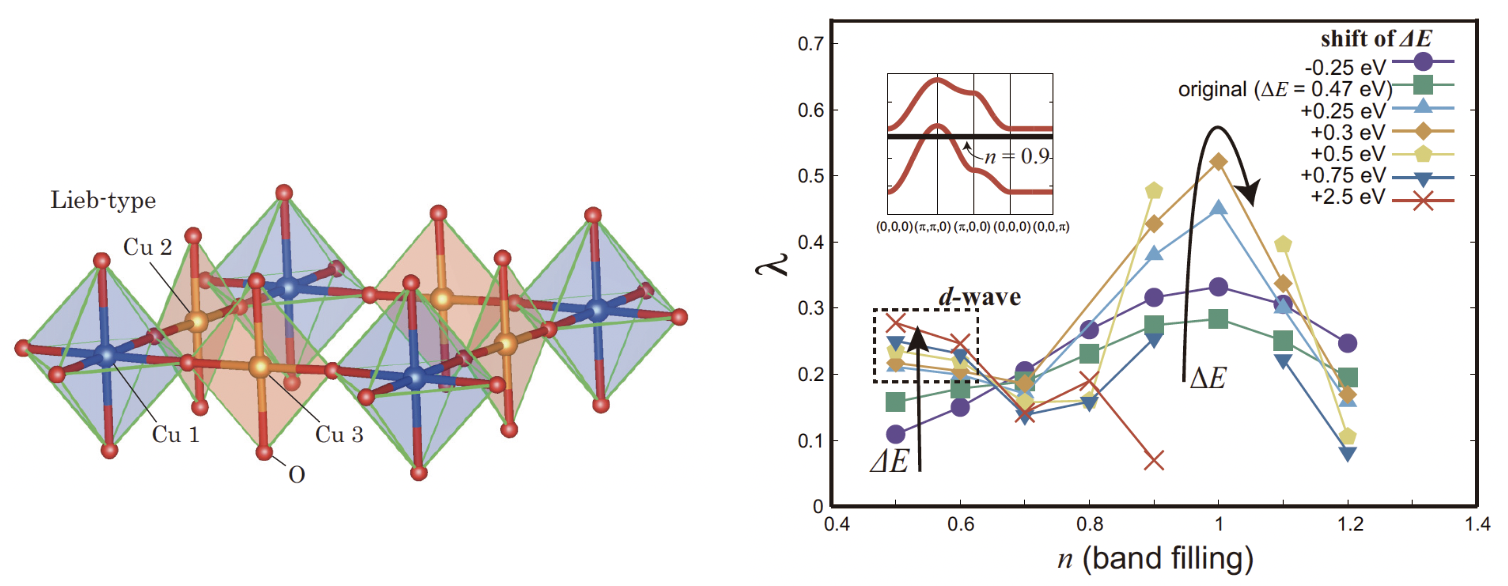
近年、新しいタイプの銅酸化物高温超伝導体として、Ba2CuO3+δが注目を集めている。通常の銅酸化物において存在するCuO2平面から多くの酸素が欠損し、かつ、多量のホールがドープされていることがわかっており、なぜ70Kを超えるTcが実現しているのか、謎となっている。我々は、結晶構造が実験的にわかっていないこの物質に対して、強磁性の研究で有名なLieb格子と類似の結晶構造を提案して、その多軌道模型に基づいて超伝導機構に関する研究を行った。その結果、軌道間相互作用が重要な役割を果たす超伝導機構が2 種類存在しうることがわかり、特に、d3z2-r2軌道を主起源とするincipient なバンドとdx2-y2軌道を主起源とするバンドが共存することによって、スピン揺らぎを起源として非常に高い超伝導転移温度が実現する可能性を見出した。従来、多軌道系におけるスピン揺らぎ媒介型超伝導においては軌道内相互作用が重要と考えられてきたのに対して、軌道間相互作用が重要や役割を果たす新しい可能性を提唱するものである[K. Yamazaki et al., Phys. Rev. Research 2, 033356 (2020), 山崎公裕, 他, 固体物理 56, 315 (2021)]。
超伝導転移温度を飛躍的に増強する機構として、2 バンド系において、一方のバンドの上端または下端がフェルミ準位のごく近傍に位置する状況(incipient band) におけるバンド間ペア散乱機構を提唱している。2 本鎖梯子型格子や2 層型正方格子上のハバード模型に対してFLEX 近似を適用し、incipient band の状況においては超伝導を抑制する低エネルギースピン揺らぎが弱くなる一方、超伝導を増強する中程度の有限エネルギースピン揺らぎが大きくなることに起因して、超伝導が飛躍的に増強されることを見出した[K. Matsumoto et al., J. Phys. Soc. Jpn. 89, 044709 (2020)]。
また、多変数変分モンテカルロ法による超伝導相関関数の計算結果を、FLEX近似によるエリアシュベルグ方程式の固有値の計算結果と比較することにより、弱相関領域から強相関領域にいたるまで、上記の描像が成立していることを示した[D. Kato, K. Kuroki, Phys. Rev. Research 2, 023156 (2020)]。
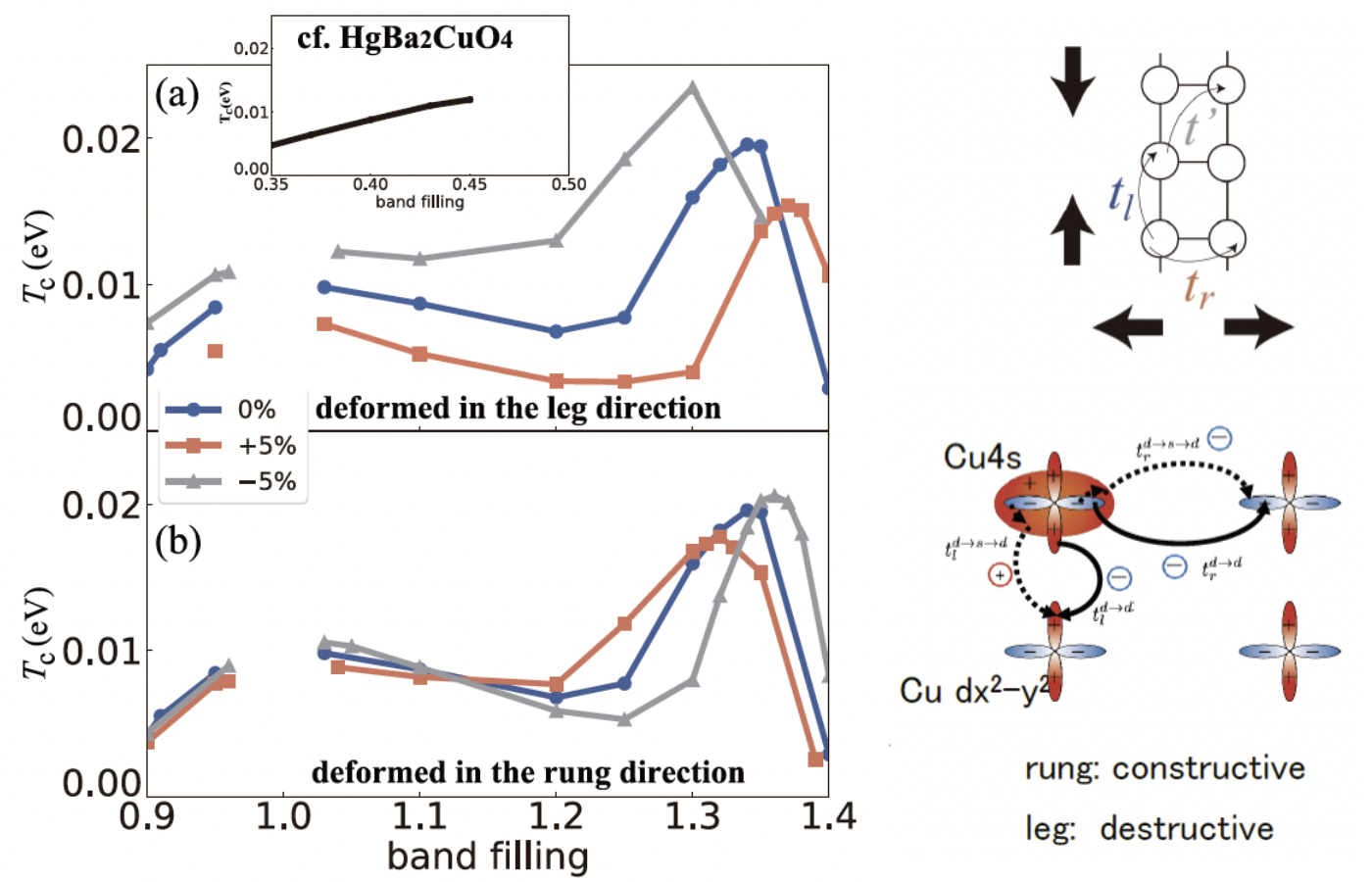
2 本鎖梯子系においてincipient band に近い状態を実現するには、梯子の横木(rung) 方向の電子のホッピングを大きくすればよい。2 本鎖梯子系においてrung 方向の電子のホッピングを大きくするには、直観的にはrung 方向に一軸的な圧力をかければよいと期待される。しかし、実際に2 本鎖梯子型銅酸化物に対して第一原理計算を行なってみると、直観とは逆に、梯子の脚(leg) 方向に圧力をかけるとよいことがわかった。ワニエ基底の構築による多軌道タイト・バインディング模型の解析の結果、これは、銅の4s 軌道が3d 軌道とオンサイトで混成することにより、複数の電子のホッピングが干渉する効果であることがわかった[H. Sakamoto, K. Kuroki, Phys. Rev. Research 2, 022055(R) (2020)]。
銅酸化物における高温超伝導の発見以降、類似する電子状態を持つ可能性のある物質の探索は極めて精力的に行われてきた。その一つとして、無限層と呼ばれる構造を持つLaNiO2がある。この物質は、珍しいNi1+の価数状態、すなわち、3d電子が9つある状態になることが期待され、銅酸化物におけるd8電子配置のCu2+の電子状態と類似する可能性がある。しかし、長らく、物質合成の報告はあるものの、超伝導の報告はなかった。ところが、2019年9月、米国スタンフォード大学グループは、LaNiO2と同類の物質NdNiO2、ならびに、これにホールをドープしたNd0.8Sr0.2NiO2の薄膜を合成し、後者において最大Tc約15 Kの超伝導を発見した。我々は、2010年ごろからLaNiO2の超伝導の可能性を理論的に研究していたこともあり、超伝導発見の報を受けて、すぐに理論の論文を著し、以下の点を論じた。すなわち、母物質においてはNdのdバンドに電子があり、Niの3dx2-y2軌道は完全なhalf-filledにはならずにわずかにホールが入るため、反強磁性にも超伝導にもならないこと、また、Niの3dx2-y2軌道の局在性が強いため、オンサイト相互作用Uが銅酸化物よりも大きく、このことが銅酸化物に比べてTcを下げる要因になっていることを指摘した[H. Sakakibara et al., Phys. Rev. Lett. 125, 077003 (2020)]。
BiS2系化合物は超伝導体として知られており、我々はその電子状態や超伝導性についてこれまで調べてきた[H. Usui et al., Phys. Rev. B 86, 220501(R) (2012). K. Suzuki et al., Phys. Rev. B 96, 024513 (2017)]。近年、その低い熱伝導率に起因した高い熱電性能にも注目が集まっている。そこで第一原理計算によってその電子状態を調べた。本物質では、BiS2伝導層において、p軌道の異方性に起因した擬一次元的電子状態が実現しているとみなせる。Biをより軽い元素、Sをより重い元素へと置換していくことで、その異方性を強められることを明らかにした。そうして異方性の強まったバンド構造は、擬一次元的gapped Dirac coneという、熱電物質において理想的な電子状態の一つであることを見出した。例えばLaOAsSe2という仮想物質を考えると、非常に高い熱電性能が期待されることも示した[M. Ochi et al., Phys. Rev. Appl. 8, 064020 (2017)]。
さらに4層系の類縁物質においても、様々な組成に対するバンド計算を実行し、高い熱電性能を実現するための物質設計指針を探った。その結果、異なる層のバンドが互いに混成することによって、バンド端がより平らに近づくバンド変形が起きうることがわかった。こうしてできるバンド構造はある種プリン型構造としての特徴を強めたものであるともいえる[K. Kurematsu et al., J. Phys. Soc. Jpn. 89, 024702 (2020)]。
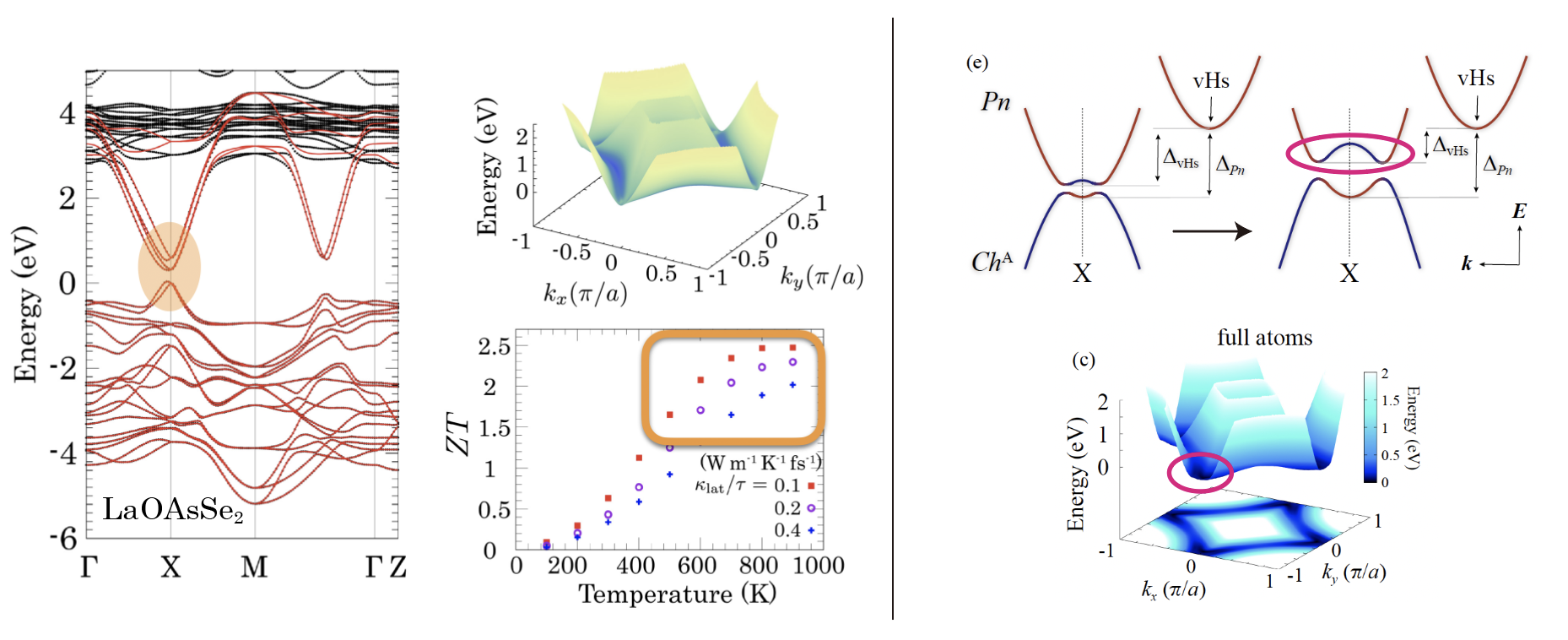
SnSeにおいて非常に高い無次元性能指数ZT=2.6が報告され、注目を集めている。我々はSnSeに対する第一原理バンド計算を行った。その結果、キャリアドープによってZTは現状よりも上昇することが示され、特に電子ドープによってZT>3も可能であることが示唆された。ホールドープ側の価電子帯にはプリン型バンドが存在し、これが熱電性能に有利に働く。一方、電子ドープ側の伝導帯は、一見、特徴がないバンド構造のように見えるが、実はp軌道の異方性に起因する擬一次元的なバンドが伝導帯端に存在する。このようなバンド構造は一方向に軽いことが大きなホール群速度を生み出し、他の方向にバンドが重いことで多くの状態を稼ぐことができるという点で、熱電効果に有利に働く。このような視点はこれまであまりなかったが、擬一次元的なバンド構造はプリン型バンドを広い意味に拡張したものととらえることができる[H. Mori et al., Phys. Rev. B 96 085113 (2017)]。
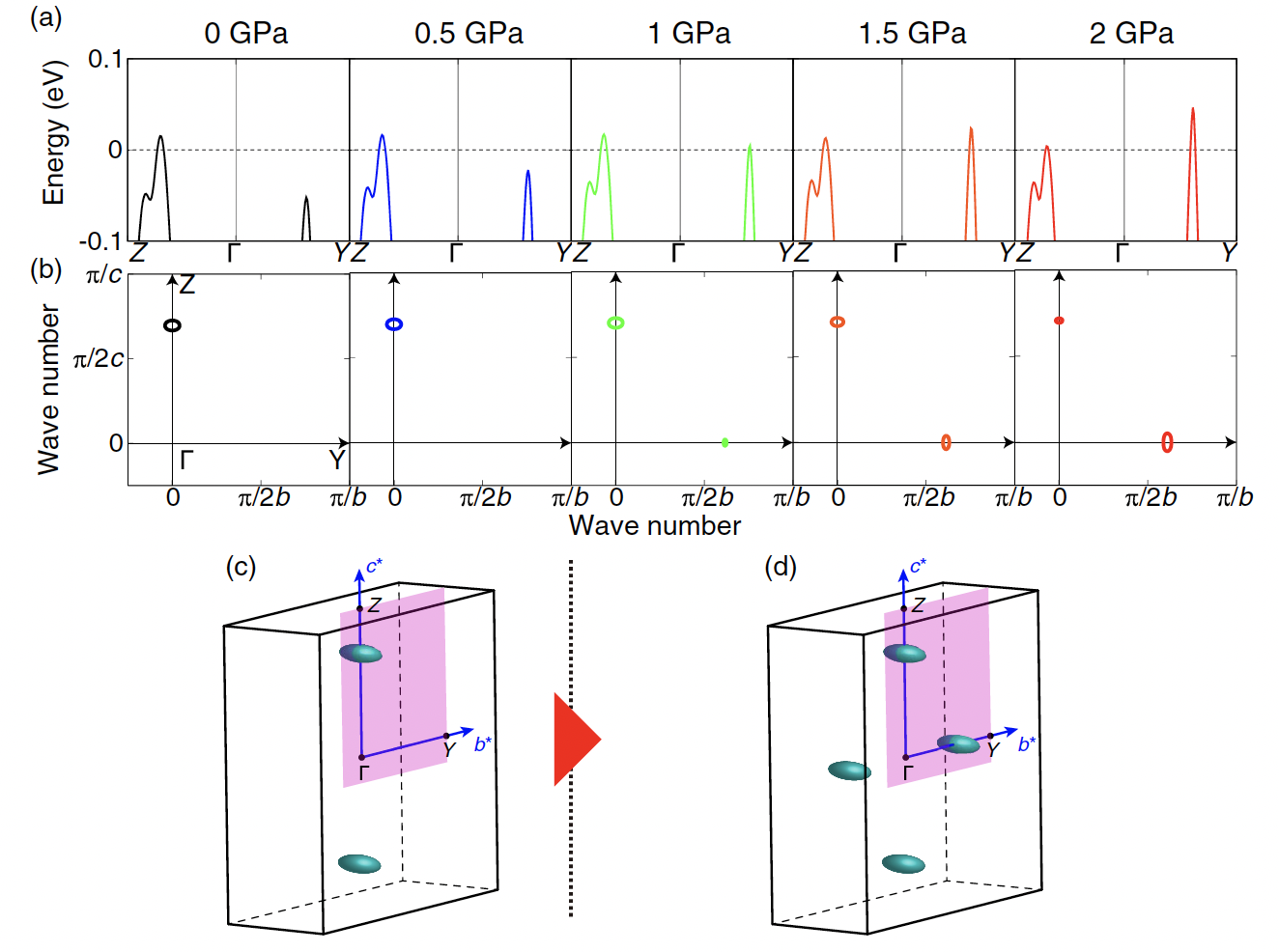
また、阪大花咲グループの実験によって、圧力印加によりSnSeの熱電性能が向上することが明らかになった。そこで、我々は理論計算によってその起源を調べた。その結果、圧力を加えることでホールバンドの数が増え、そのことが電力因子の増加に繋がったことが明らかになった。本共同研究成果はPhysical Review Letter誌に掲載された[T. Nishimura et al., Phys. Rev. Lett. 122, 226601 (2019).)プレスリリースはこちら]。
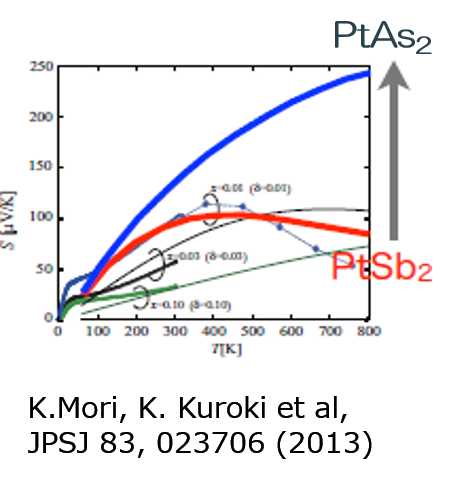
岡山大学の野原実グループによって、PtSb2が高い熱電性能を持つことが示されたのを受け、我々の研究室では、この物質の第一原理バンド計算を行い、ゼーベック係数を計算した。実験では、300K付近までは温度上昇とともにゼーベック係数が単調に増大するものの、高温では減少に転じてしまうことが見出されていた。理論計算をすると、低温での大きな熱電性能はバンド形状が優れていることに起因することがわかり、高温での減少は、バンドギャップが小さいことに起因することがわかった。
高温までゼーベック効果が単調増加すれば、さらに高い熱電性能が期待されることから、我々はPt, Sbのそれぞれの元素を考えられる可能な範囲で置換した全ての物質についてバンド計算を行い、それぞれのゼーベック係数を計算した。その結果、PtAs2においては、バンドギャップが適度に開き、かつ価電子帯のバンドの形状も熱電性能に適したものになって、ゼーベック係数は高温まで単調に増大し続けることを予測した。その後、野原グループにおいて、実際にホールキャリアーをドープしたPtAs2が合成され、理論の予想どおり、高温まで単調に増大するゼーベック係数が観測された結果、温度600Kにおいて80µW/cmK2という世界新記録レベルの高い電力因子が得られた。
1111系鉄系超伝導体LaFeAsOは、最初に発見された鉄系超伝導体であるが、その後も元素置換によってさまざまな興味深い現象が観測されている。LaFeAsOのOをFで置換することで超伝導が発現するが、フッ素置換の場合、20%程度までしか置換できない。東工大の細野グループでは、酸素を水素で置換することによって50%を超える置換に成功した。20%の置換まではフッ素置換の場合と同様のTcの置換量依存性を示し、転移温度は途中で最大となる「ドーム」を描くが、その後、再度上昇に転じて第二のドームを描くことが示された。さらに興味深いことに、LaをCe,Sm,Gdと置換すると、第二ドームが第一ドームと合流するように見受けられ、20%置換付近のTcの極小が消え、それとともに、Tcの最大値は50Kを超えるようになる。フェルミ面のネスティングが大きく崩れていると想像される高ドープ領域において高いTcが得られることは、フェルミ面のネスティングによって得られるスピン揺らぎが超伝導の起源であるというシナリオを疑問を投げかけた。
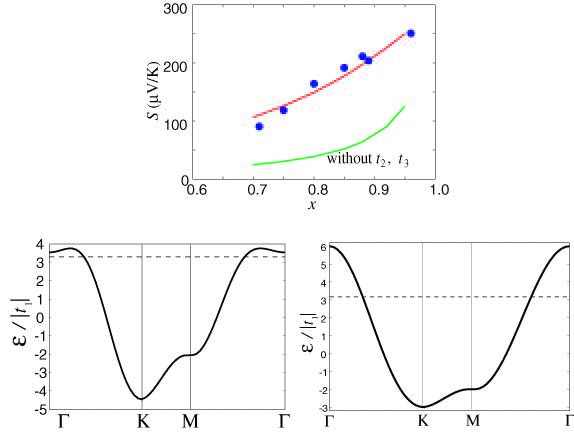
我々は、第一原理バンド計算から導出された5軌道有効模型を用いてこの問題に取り組んだ。ここで重要なことはリジッドバンドを仮定せず、元素置換の効果を、仮想結晶近似によってバンド構造によって取り込むことである。実際、水素やフッ素置換によってバンド構造が大いに変化することが示された。その主たる原因は、dxy軌道内の電子のホッピング積分の変化に起因する。置換が少ないうちは第一と第二隣接ホッピングt1, t2の大きさを比較すると前者が大きいのに対して、置換が進むにつれ、後者が大きくなるという「異常」な状態になる。この理由は、第一隣接サイトへの電子の移動経路が二通りあり、その位相が逆であるために打ち消しあいが起こるが、置換とともにその打ち消しあいが顕著になるためである。
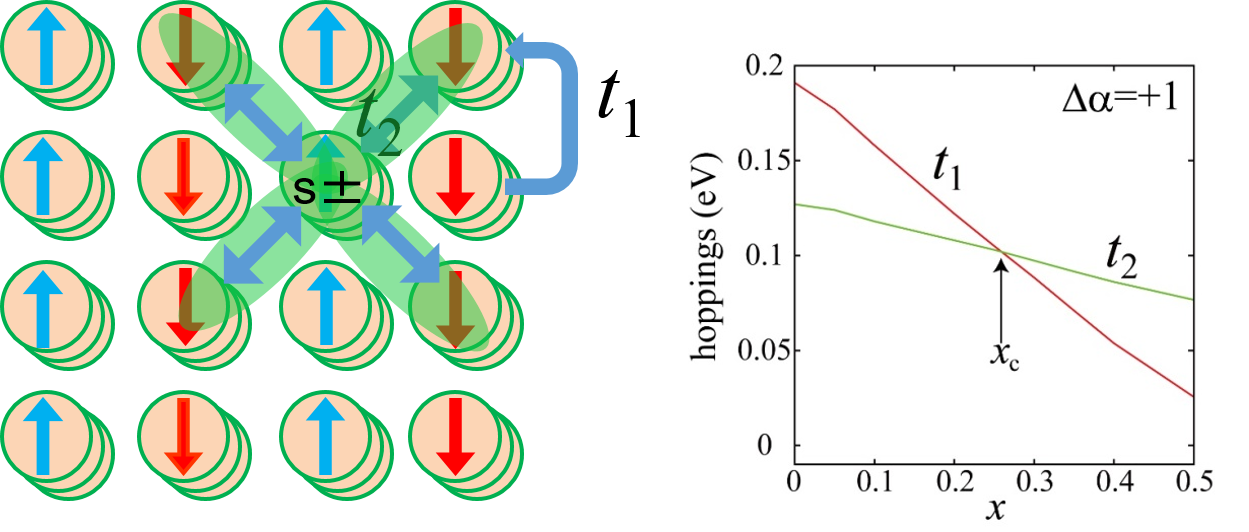
この有効模型を使って超伝導の計算を行うと、実際に置換量xの増大とともにs±波超伝導の再上昇が再現された。フェルミ面のネスティングが悪くなるにもかかわらずこのようなことが起こるのは、s±波超伝導が実空間で言うと第二隣接サイト間のペアリングに対応するため、ホッピングの大小関係の逆転が超伝導に有利に働いたためであると解釈できる。さらに、LaをSm等の小さい元素に置換すると、t1とt2の大小の入れ替わりが、少量の水素ドープで起こることがわかり、このことが第二ドームが第一ドームと合流することの起源であることもわかった。
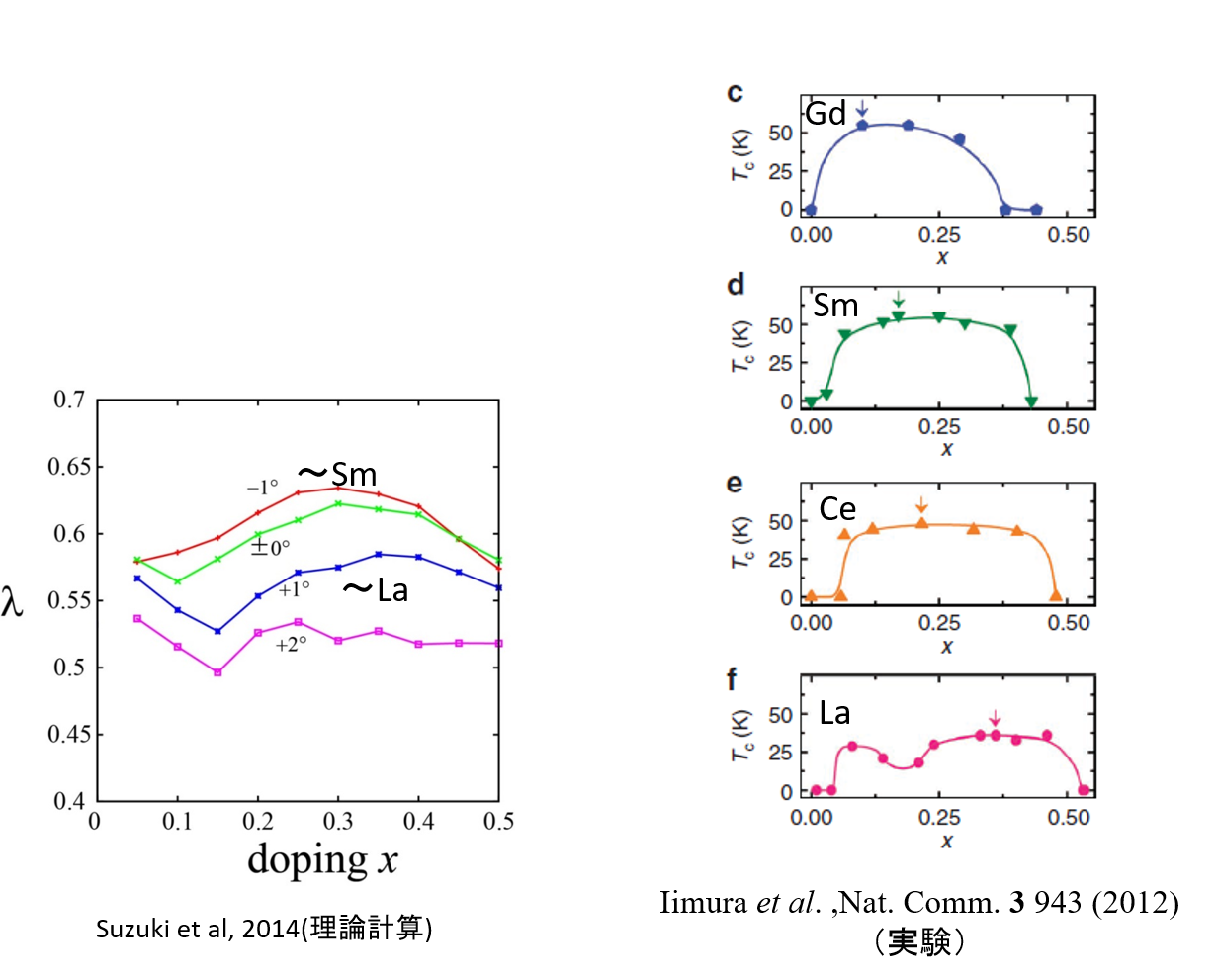
なお、鉄系超伝導においてt1<t2が第二隣接サイト間ペアリングに対応するs±超伝導に有利に働くのに対して、銅酸化物高温超伝導体においては必ずt1>t2であり、これが第一隣接サイト間ペアリングに対応するd波超伝導に有利に働いていると理解できる。このように、既存の高温超伝導体においては、実空間のホッピング積分の大小関係が波数空間(フェルミ面)のペアリング描像とマッチングがとれているという統一的理解は興味深く、あらたな高温超伝導体探索のヒントとなりうる。
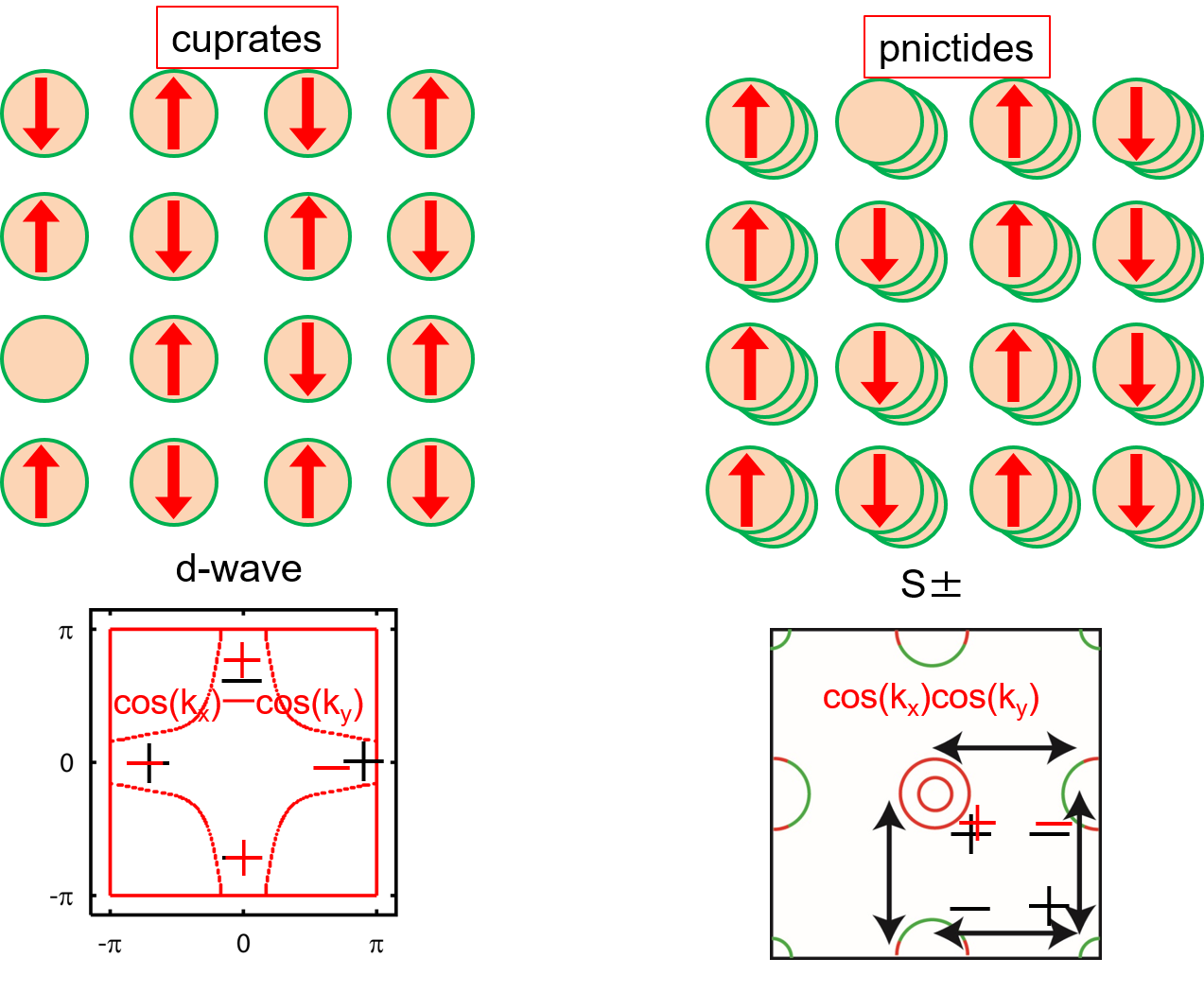
LaFeAs(O,F)は、AsをPに置換することもできる。この置換によっても、超伝導のTcが非単調なふるまいを示すことが阪大理の田島グループによって発見された。すなわち中途半端なPの量に対して、Tcが極大をとる。さらに阪大基礎工の北岡・椋田グループのNMR実験により、このTcの極大近傍において低エネルギースピン揺らぎの増大が観測された。元素置換量に対してTcの極大が複数現れる現象は、上記の水素ドープ型を連想させるものである。
我々はこのLaFe(As,P)(O,F)に対しても、元素置換の効果をバンド構造に反映させた有効模型を使った解析を行った。その結果、中途半端なリン置換量において、フェルミ面のネスティングが極めてよくなり、超伝導が極大になる領域があることがわかった。これは置換によってホール面の一つが消失することで、ホール面と電子面の数が等しくなる(ともに2枚になる)ことが一因である。しかし、置換量を増やし続けてもこの電子・ホールのフェルミ面バランスは変わらないのに、いずれ超伝導は抑制されるようになる。実はリン置換量が多くなりすぎると、ホール面と電子面とでdxz/yz軌道成分の混成の仕方が異なるようになり、電子とホールの軌道成分の一致が重要であるスピン揺らぎにとっては実質的にネスティングが悪くなった状態が実現することが、超伝導に不利に働くことがわかった。
上記のように元素置換の効果をバンド構造の変化に反映させた5軌道有効模型を用いることで、1111系鉄系超伝導体のTcの元素置換量依存性を包括的に理解することができた。その概念図を以下に示す。
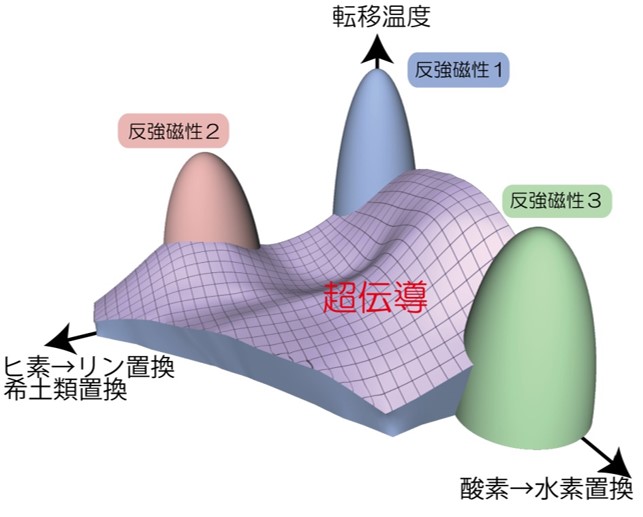
我々がNaxCoO2における大きな熱電効果の起源として提唱した「プリン型バンド」は、様々な既存熱電物質、あるいは熱電物質の候補でみられることがわかってきた。我々が研究対象としてきたものを、以下の図にまとめた。
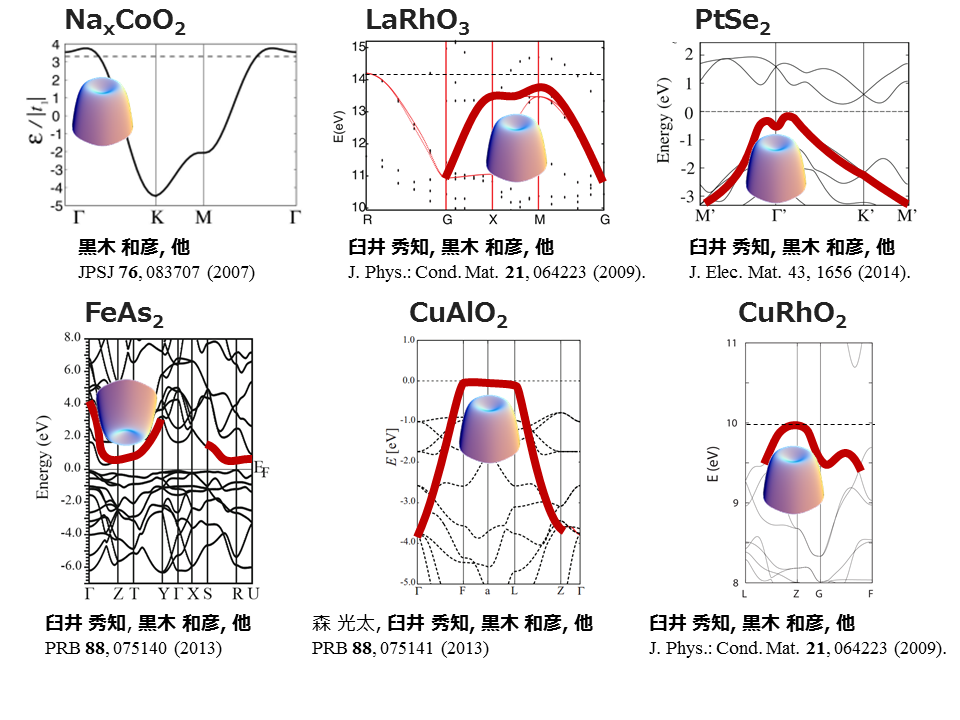
東京工業大学の細野秀雄氏らのグループにより鉄系ニクタイド、F-doped LaFeAsOが26Kの超伝導になることが発見された。その後、ランタノイド置換による同族の化合物も数多く合成され、今やTcは50Kを超え、その超伝導メカニズムに興味が持たれる。我々はまずLaFeAsOに対して第一原理バンド計算を行い、そこから最局在ワニエ軌道を得ることで、3dバンドに対するタイト・バインディング模型を構築した。AsがFeの周りに正四面体配置をとるために単位胞内には二つのFeが含まれ、3dバンドだけでも10バンド模型となる。しかし、各Feの周りの局所的なAs配置が等価であるため、Fe一つのみを含む単位胞に取り直すことができ、その結果5バンド模型を得ることができる。5つのバンドは複雑に絡み合っており、第一原理計算のフェルミ面を正しく再現するには5つの軌道を全て考慮した模型が必要であることがわかった。フェルミ面は図のように(0,0)周りに二つ(α1,α2)、(π,0),(0,π)周りにそれぞれ一つづつ(β1, β2)存在する。また、(π,π)近傍はバンドがフェルミ準位に極めて接近しており、有効的にフェルミ面(γ)的な役割を果たしうる。α1,α2とβ1, β2のブリルアンゾーン境界付近はxz, yz軌道、β1, β2のブリルアンゾーン境界から離れた箇所とx2-y2軌道の性格が強い。
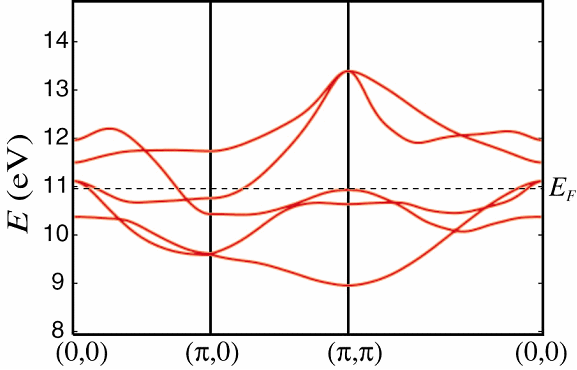
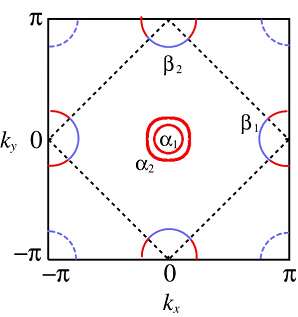
次に、上記一体項に加えて、軌道内及び軌道間の電子間相互作用を考慮した多体模型をRPA法により調べた。その結果、α-β間、及びβ-γ間のフェルミ面のネスティングにより下図のように(π,0),(0,π)のスピンの揺らぎが発達することがわかった。ドープされていない母物質においては、この波数を持つスピン秩序が中性子による実験で観測されており、整合しているといえる。さらに、RPAで得られたスピン・電荷感受率を用いたエリアシュベルグ方程式により、超伝導を議論した。ギャップは5×5の行列になるが、図に軌道表示でのギャップ関数の対角成分を示す。ギャップは拡張s波対称性を有しているが、スピンの揺らぎに起因する超伝導であるため、フェルミ面のネスティング・ベクトルの始点と終点の間でギャップの符号が反転している。また、軌道別に見ると、x2-y2軌道のギャップが大きくなっており、この軌道が超伝導の主役を担っていることがうかがえる。本研究成果はPhysical Review Letter誌に掲載され[Phys. Rev. Lett. 101 (2008) 087004]、日経新聞、日経産業新聞、日刊工業新聞においても取り上げられた。
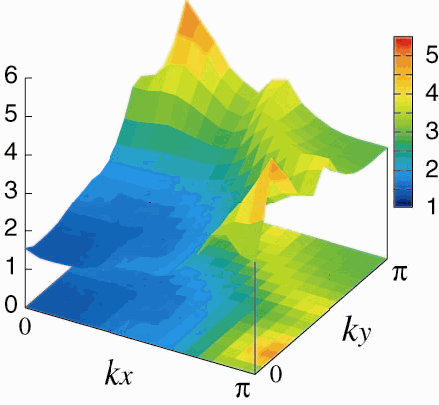
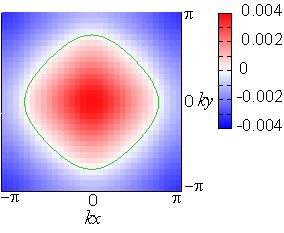
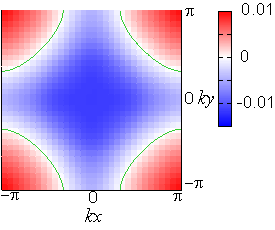
鉄系超伝導体については、発見からまもなくして、その物質依存性が注目されるようになった。LaFePOにおいては臨界温度は5K程度と低いのに対して、NdFeAsOやSmFeAsOにおいては50Kを超える。のみならず、LaFePOにおいては、超伝導ギャップにノードがあることが様々な実験から観測されている。臨界温度は結晶構造と強い相関があることが示され、特に、Fe-As-Feの結合角との相関関係が指摘された。
我々は、これらの実験事実を理解するために、現実の物質構造を用いて行ったバンド計算をもとに5軌道模型を構築し、その超伝導を調べた。文献Phys. Rev. B 79 (2009) 224511においては、鉄原子が構成する層から測ったニクトゲン原子の高さに着目し、LaFePOのように高さが低いときには(π,π)回りにフェルミ面がない(あるいは3次元的なフェルミ面のみ)が、NdFeAsOのように高さが高くなるにつれて波数(π,π)回りにフェルミ面が出現することを指摘して、その有無に応じて、臨界温度の低いnodalな超伝導と臨界温度の高いnodelessな超伝導の切り替えが起こることを指摘した。
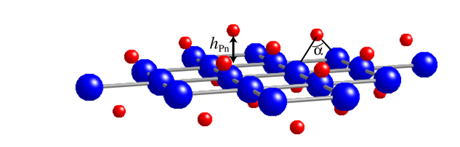
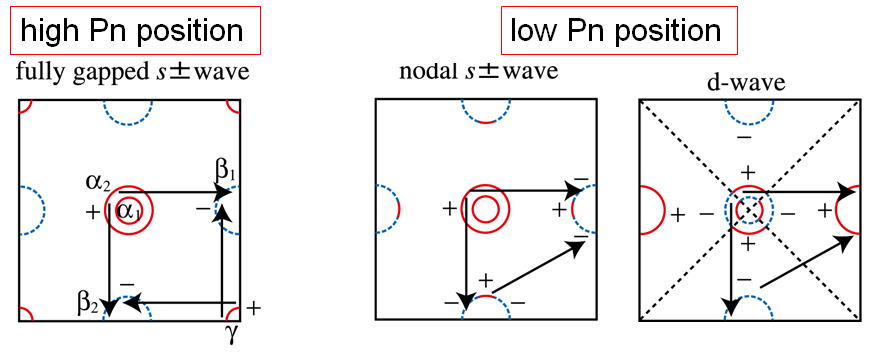
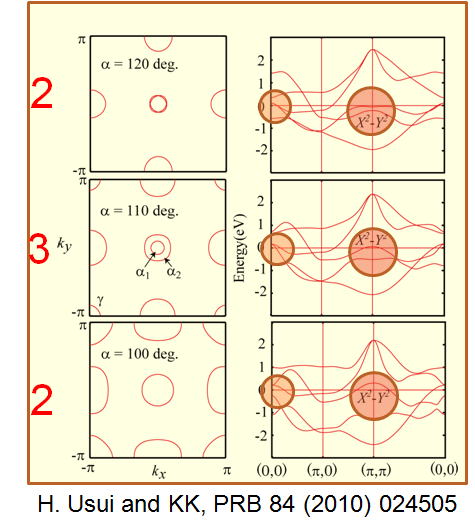
上記の理論の範囲内においては、ニクトゲンの高さが高くなるにつれて、臨界温度が高くなることは理解できるが、実験においては、ニクトゲンの高さやFe-As-Fe結合角には最適値ががあり、特に結合角はニクトゲンが正四面体構造をとる付近が最適とされる。このことを理解するために、文献Phys. Rev. B 84 (2011) 024505においては、結合角が小さくなりすぎると波数(0,0)まわりに2枚存在していたホール面のうちの1枚が消失することに着目して、超伝導の研究を行った。結合角を大きいほうから小さくしていくと、フェルミ面枚数が2->3->2と変化し、正四面体結合角付近でホール面枚数が3枚となって最大化される。これに伴って、超伝導の転移温度も正四面体構造近傍で最適化されることを示した。
鉄系超伝導体のなかでも、BaFe2As2のようないわゆる122系は、3次元性が比較的高い物質群である。フェルミ面も3次元性が強く、また、体心正方格子という結晶構造に起因して、LaFeAsO等の1111系で理論的に行われてきたブリルアン・ゾーンのunfoldingが厳密にはできない。
我々は、122系に対して、バンド構造を正確に再現する10軌道模型、ならびに、近似的にunfoldして得られる5軌道模型を用いてスピン揺らぎと超伝導の研究を行っている。BaFe2(As,P)2やKFe2As2においては、超伝導ギャップにノードが観測されており、その起源として、122系特有の強い3次元性を持ったフェルミ面に水平方向(horizontal)に入るノードの可能性を提唱した[J. Phys. Soc. Jpn. 80 (2011) 013710, Phys. Rev. B 84 (2011) 144514]。
また、鉄系超伝導体全体において観測されている、スピン揺らぎの非整合性のドープ依存性の電子・ホール非対称性の起源について、122系の近似的な5軌道模型を基に解析し、フェルミ面が複数の軌道成分からなっていることが原因であることを指摘した[Phys. Rev. B 84 (2011) 144514, Phys. Rev. Lett. 106 (2011) 067003]。
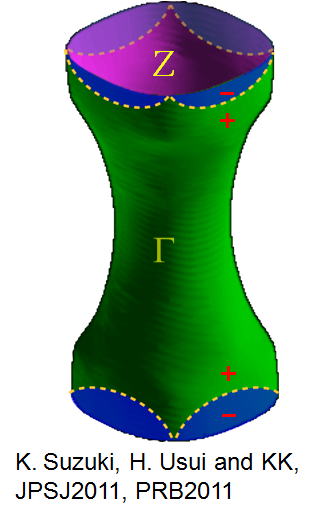
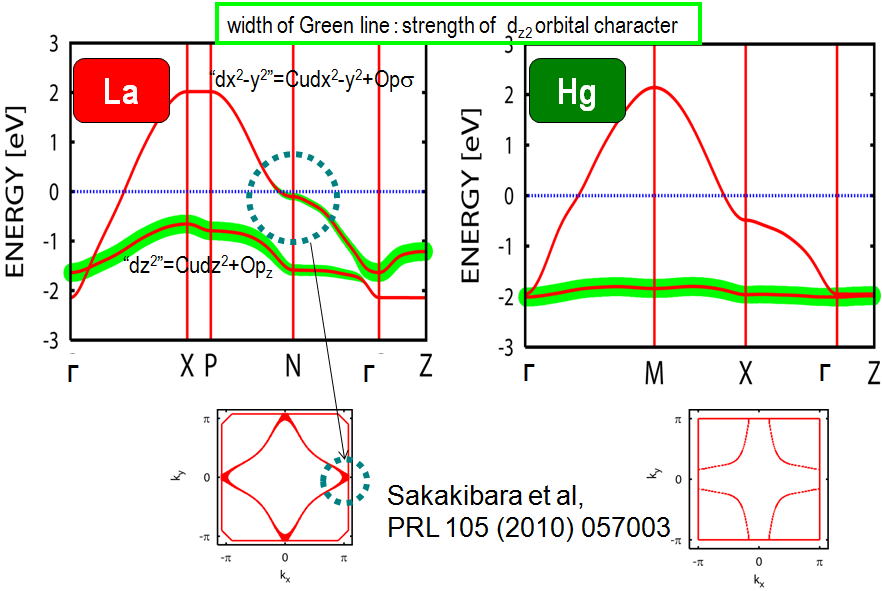
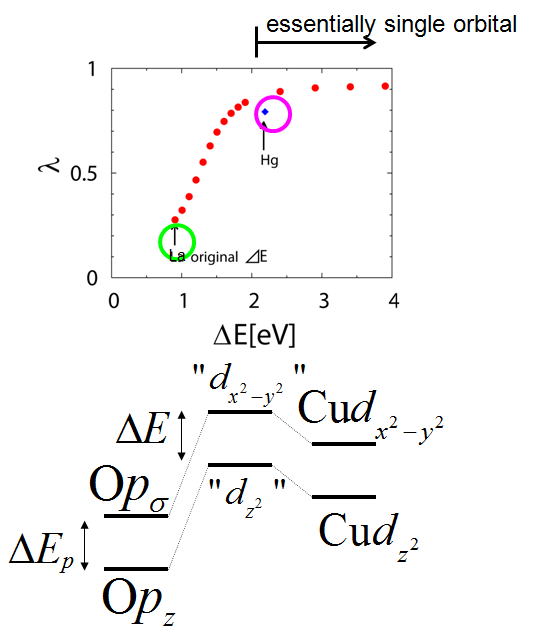
銅酸化物は高い臨界温度を示す高温超伝導体として知られるが、その中でも臨界温度の物質依存性がある。単位胞内にあるCuO2層の枚数によって臨界温度が変化することはよく知られているが、単位胞内にCuO2を一層のみ含む、「一層系」のなかでも、ランタン系は最大~40K、水銀系は100K近くと、大きな物質依存性がある。我々は一層系における臨界温度の物質依存性の起源を理解するために第一原理計算から構築した2軌道模型を導入した(図1)。従来の研究においては、フェルミ面の形状のみによって、物質依存性を理解しようとする研究が大勢であったが、このような視点に立つと、実験的に観測されるフェルミ面形状と臨界温度の相関関係は一見、理解しにくいように思われる。ところが2軌道模型を考え、軌道間のエネルギー差の違いによって、フェルミ面形状が制御されていることを考慮すると、実験的に観測されている臨界温度の物質依存性が自然に理解できることを示した[Phys. Rev. Lett. 105 (2010) 057003]。
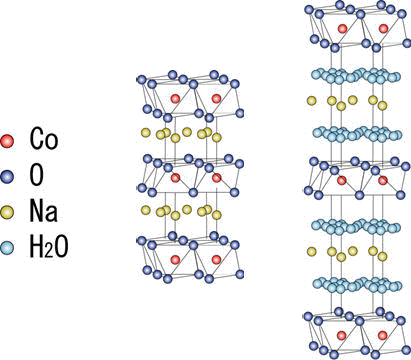
コバルト酸化物NaxCoO2は 大きな熱起電力にはじまり、磁性、そして水和物における超伝導と、興味深い現象が次々と発見され、おおいに注目をあびてきた。熱電効果や超伝導は基礎物理のみならず、エネルギー問題等にも結びつきうる重要な物理現象であり、その意味でも興味深い。そして、これらの三現象を最初に発見したのはいずれも日本人であり、まさに日本発の物質といえるが、これらの発見以降、世界中で実験、理論の両側面から精力的に研究が行われている。
水和物における超伝導についてはスピンの揺らぎが関与した、非従来型超伝導の可能性が高いことが様々な実験から示唆される。また、この物質のバンド構造をみると、3重縮退したt2g軌道はa1gとeg’に分裂するが、角度分解型光電子分光の実験によると、後者のバンドはフェルミ準位以下に沈んでいることが観測されている。そのため、a1gバンドが重要な役割を演じている可能性が高い。我々はa1gバンドがΓ点に極小構造を持つ(図)ことから、内側と外側の二重フェルミ面が形成されている可能性があることを指摘し、二つのフェルミ面の間のネスティングから非整合波数を持つスピン揺らぎが発達すること、そしてこの揺らぎを媒介として、二つのフェルミ面間でギャップの符号が変わる非従来型拡張s波超伝導が発現しうることを、2次元拡張ハバード模型に対するFLEX近似計算を用いて示した[Phys. Rev. B 73 (2006) 184503]。磁性については、伝導が金属的であることから、遍歴描像が必要であると考えられる。また、水和物に比べると3次元性が強いことから、我々は3次元ハバード模型を採用した。ここでもa1gバンドのΓ点での極小構造が重要となる。このバンド構造に起因して3次元的なフェルミ面に内側部分と外側部分が生じ、Na量が多いとき、その間に(0,0,π)をネスティング・ベクトルとするネスティングが生じる。これに起因して、中性子散乱の実験と整合する面内強磁性、面間反強磁性のスピン相関が発達することをFLEX近似を用いて示した。そして、磁気転移温度、スピン波の分散等を計算し、実験と定量的に整合することを示した[Phys. Rev. Lett. 98 (2007) 136401]。

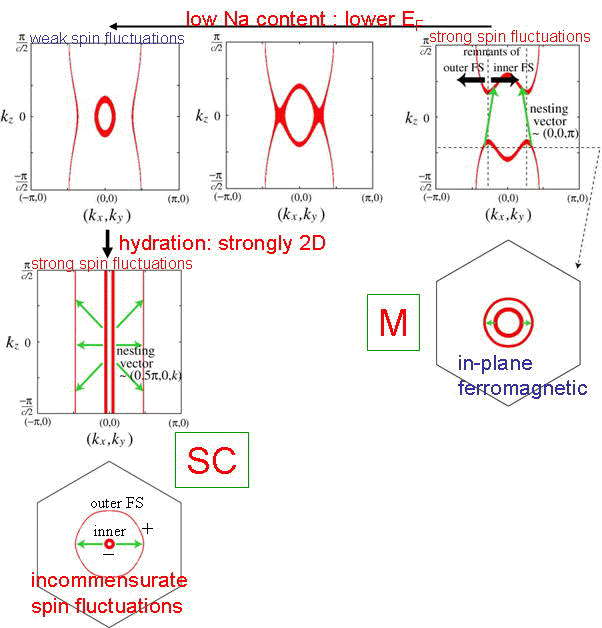
超伝導、磁性ともにa1gバンドの単一バンド理論でかなりの部分が理解できることから、さらに、熱電効果についても単一バンドの見地から考えた。ここでもa1gバンドの形状が重要となる。a1gバンドの上端部分はΓ点周りで比較的平らになっており、Γ点からある程度離れるたところから急激に分散をもつような形状をしている。この形状を我々はプリン型と名付けた。プリン型バンドの特徴は、バンドの曲がり角付近にEFがあると、(i) EFの上下で群速度が大きく異なるため熱起電力が大きくなる、(ii)キャリアー数を小さくして熱起電力を大きくした場合と違って、EFの下で群速度が大きく、フェルミ面も大きいことから電気抵抗も比較的小さくなり得る、という点である。このため大きな熱起電力と小さな電気抵抗の両立が可能となり、応用上重要となるpower factorが大きくなる。実際、NaxCoO2はこの二者の両立が成立する点が不思議と考えられていた。図に示すように、a1gバンドのプリン型分散を考慮した計算によって、熱電効果の実験を定量的に説明することができる。この成果はJ.Phys.Soc.Jpn.に掲載され、編集委員会が選ぶ注目論文 "Papers of Editors' Choice"に選ばれた[J. Phys. Soc. Jpn. 76 (2007) 083707]。また、この研究成果は2007年8月31日発行の科学新聞に掲載された。日本物理学会誌にも「最近の研究から」として掲載され、FSST NEWSにも「トピックス」として掲載された[日本物理学会誌 63 (2008) 195, FSST NEWS No.116 (2008)]。
以上により、NaxCoO2における超伝導、磁性、大きな熱起電力という3つの物性は、a1gバンドの特殊な形状に起因していると理解することができる。特に超伝導については、我々がこれまで一般的に提唱してきた非連結フェルミ面による超伝導[Phys. Rev. B 64 (2001) 024501, Phys. Rev. B 66 (2002) 184508]、あるいはnarrow-band&wide-band共存系の超伝導[Phys. Rev. B 72 (2005) 212509]の一例とみることができ、また熱電効果についての理解は、第一原理バンド計算を用いて熱電材料を設計をする上での新しい指針を与え得るものと考えられる。
上記熱起電力の理論の一般性を調べるために、同様に金属的性質を示しながら、熱起電力の大きないくつかの物質において、第一原理バンド計算を行い、ゼーベック係数の計算を行った。 LiRh2O4においてはLMTO法により第一原理計算を行い、まずボツルマン理論によりゼーベック係数を計算した。その結果、実験結果を20%ほど上回るものの、パラメーターレスの計算としてはかなり一致する結果を得た。ここでも、バンドの群速度を計算してみると、バンド上端でバンドが平らになるプリン型形状の傾向があることがわかった。また、このプリン型バンドが二重に重なっていることがNaxCoO2ほど大きな熱起電力に結びつかないこともわかった。さらに、電子相関の寄与を正確に取り込むために、DMFTの計算を行って自己エネルギーを評価し、久保公式によってゼーベック係数を計算した。その結果、ゼーベック係数はボルツマン理論で計算したものよりも小さくなり、実験結果とさらに合う方向となった。LaRhO3については平面波基底による第一原理バンド計算を行い、ボルツマン理論によりゼーベック係数を計算した。実験的にはNiドープにより金属性が増してもゼーベック係数が減少せず、それにともなってpower factorが単調増加するという結果が得られているが、この傾向を再現することができた。これは結晶構造が理想的な立方ペロブスカイト構造からゆがむことによってバンド縮退が解けることと、バンドの頭の部分が平らになることによって理解できることがわかった。その他、CuRhO2についても第一原理計算+ボルツマン理論により計算を行い、実験で得られているゼーベック係数の温度依存性を1000K付近まで再現できた[J. Phys.: Cond. Matt. 21 (2009) 064223]。これらは雑誌「固体物理」において「トピックス」として掲載され[固体物理 43 (2008) 569]、またNTS社より刊行予定の「熱電変換技術ハンドブック」にも掲載される。
銅酸化物においては通常、CuO2面によって超伝導が起こる。そのため、それ以外の構造を持つ銅酸化物において超伝導が見つかることは大変興味深いと同時に、銅酸化物における超伝導機構の理解に役立つ。そのような物質としては梯子形(14-24-41系)があるが、あらたに、Pr2Ba4Cu7O15-δが加わった。酸素をある程度の量還元すると最大で20K程度の超伝導が生じることが新潟大学を中心とするグループにより発見された。この物質は2次元CuO2面がPr系特有の効果により絶縁体化しており、超伝導になるのは二重鎖構造の部分であると考えられている。
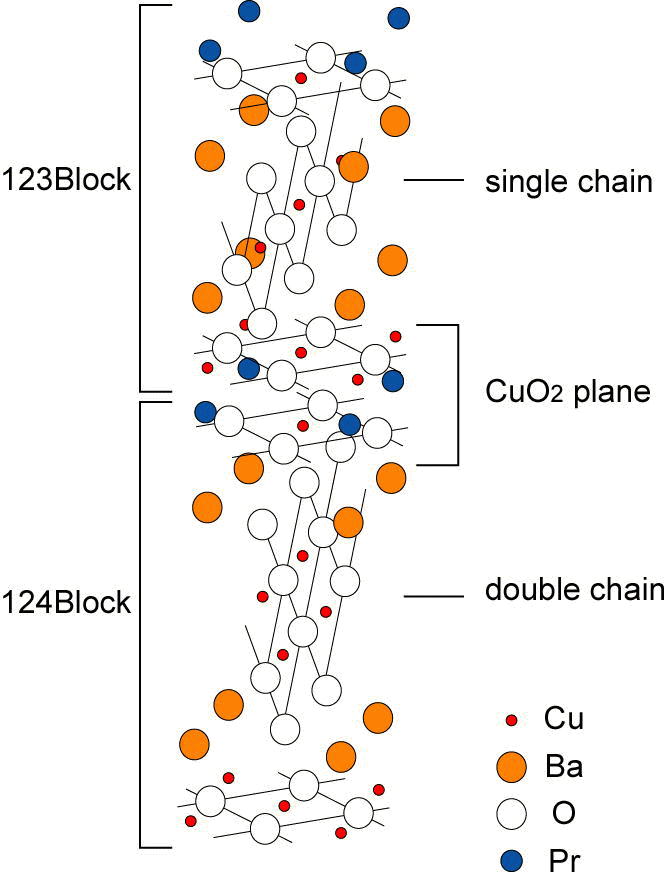
我々はこの物質の第一原理バンド構造のうち、二重鎖からくる部分を再現する擬一次元tight binding模型を構築し、FLEX近似により超伝導の可能性を検討した。この物質のバンドの特徴は、バンドの非単調な形のために、擬一次元的なフェルミ面の内側と外側の二重構造になる点である。
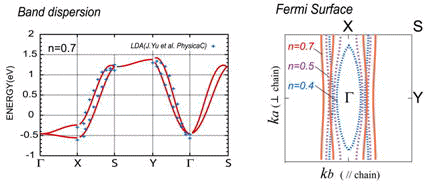
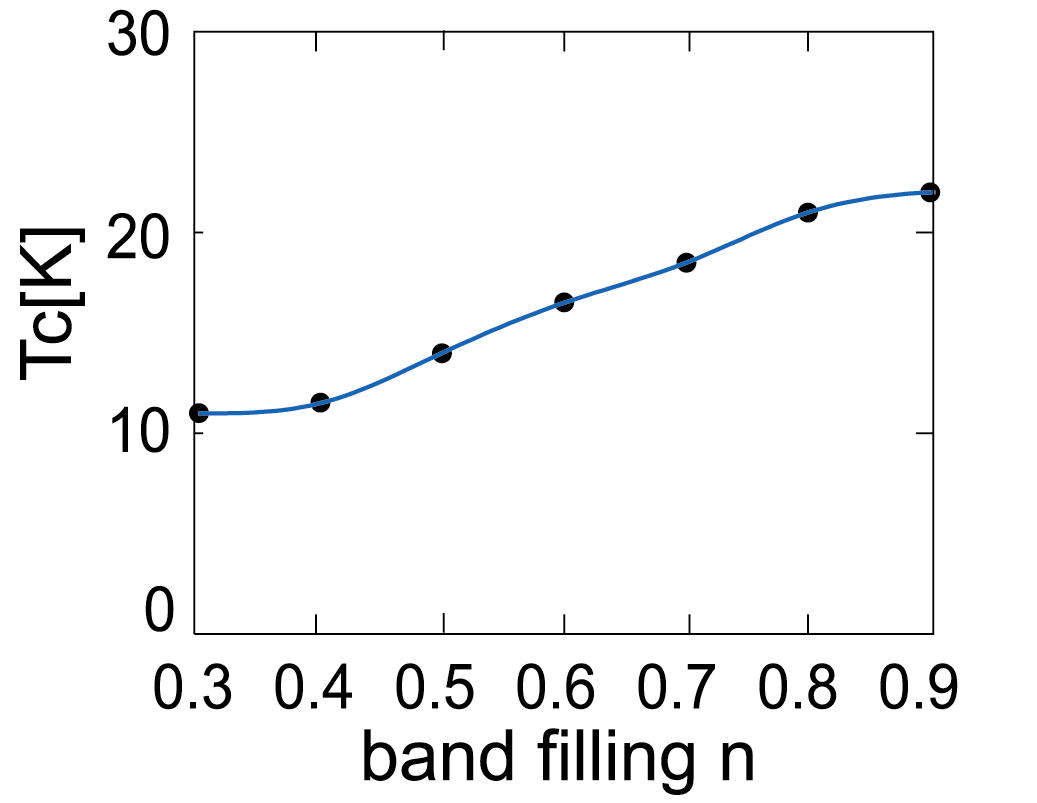
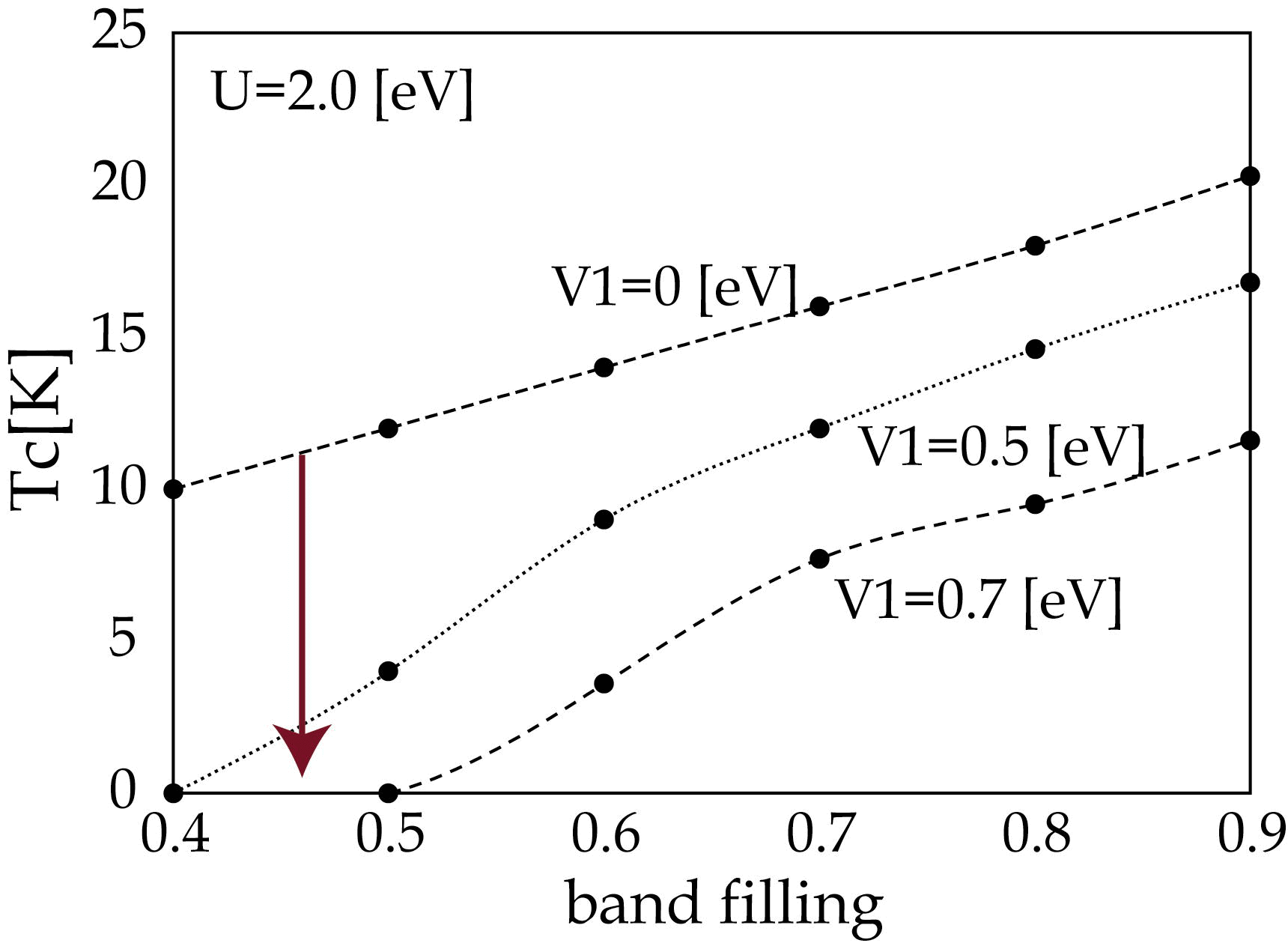
オン・サイトの相互作用Uのみを考える模型では、内側と外側のフェルミ面のネスティングにより、スピンの揺らぎが発生し、20K程度の現実の実験結果と近いTcを与える。ただし、Tcのバンド・フィリング依存性があまり大きくないことが、還元しないと超伝導にならないことと整合しない。そこで、さらに隣接サイト間相互作用Vも考慮した。これによりδ=0(電子のバンド・フィリングでいうとquarter-filled近傍)におけるTcが消失し、実験と整合する結果を得ることができる[Phys. Rev. B 76 (2007) 014515]。
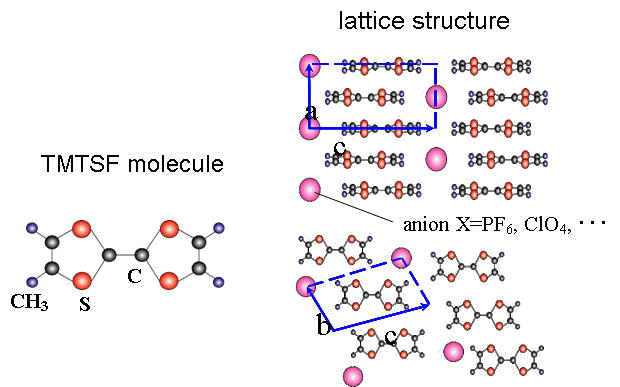
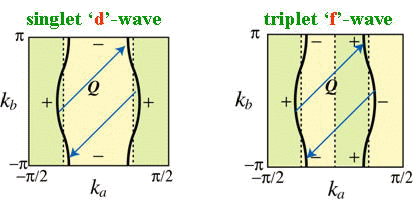
擬一次元的な有機超伝導体であるTMTSF塩においては臨界磁場やNMRのナイトシフトの実験などから、スピン・トリプレット超伝導の可能性が指摘されている。しかし、圧力-温度の相図上、超伝導はSDW相に隣接するため、単純にはd波的なシングレット超伝導が理論的に予想され、実験と整合しない。トリプレットp波超伝導の可能性は以前より指摘されてきたが、通常はp波超伝導とSDW揺らぎ(反強磁性的な揺らぎ)は相容れない。そこで我々はこの物質のフェルミ面の擬一次元的な性質に着目し、スピン・トリプレットf波超伝導の可能性を提唱してきた。すなわちフェルミ面が非連結であるため、f波とd波でフェルミ面を通過するノードの数が同じであり(図)、さらに2kFのスピンの揺らぎと2kFの電荷揺らぎが同程度の大きさで共存する場合にはシングレット・ペアリング相互作用とトリプレット・ペアリング相互作用の絶対値が等しくなるため、f波とd波超伝導が拮抗する。実際、PF6塩においては2kFのSDWとCDWの共存が実験的に観測されており、f波トリプレットのシナリオの可能性を示唆する。我々はまずはじめにスピンの揺らぎと電荷の揺らぎを現象論的に取り扱った議論を行い相図を得た[Phys. Rev. B 63 (2001) 094509, J. Phys. Soc. Jpn. 75 (2006) 051013]。
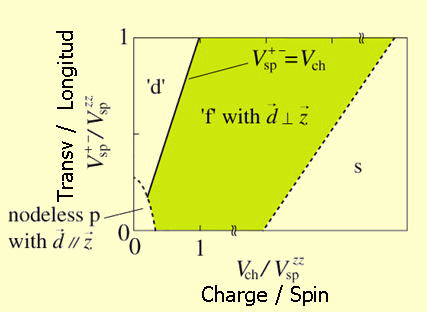
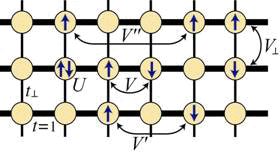
さらに微視的な模型を設定し、乱雑位相近似を用いて上記の現象論的な議論を検証した。2kFスピン揺らぎと2kF電荷揺らぎが共存するためには、鎖内第二隣接のオフサイト斥力相互作用が重要であることが、これまでの小形らのグループの研究によってわかっているので、第二隣接相互作用V’を考慮した拡張型ハバード模型を考えた。計算の結果、2kFスピン揺らぎと2kF電荷揺らぎの強さが同程度以上になるのはV’≧U/2 (Uはオンサイト斥力)のときであり、このときf波超伝導がd波超伝導に勝って出現することがわかった[Phys. Rev. B 70 (2004) 060502(R)]。ただし、V’≧U/2という比較的大きな第二隣接サイト間相互作用が現実の物質において実現可能であるか、という問題が残る。そこで、次のステップとして鎖間の斥力相互作用V⊥をも考えた(図)。一次元性の強い物質であるので鎖間相互作用は通常無視されることが多いが、鎖間の距離はそれほど離れているわけではないので、電子のとび移りが小さくても鎖間のクーロン相互作用は比較的大きいと考えられる。
このときに上記と同様の計算によってf波超伝導とd波超伝導の競合を調べた結果、f波がd波に勝るための条件はV’ + V⊥ ≧U/2と変更され、現実的なパラメーター領域でf波超伝導になりうることがわかった(図)[J. Phys. Soc. Jpn. 74 (2005) 1694-1697]。
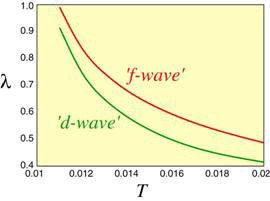
乱雑位相近似のような近似理論と併用して、有限サイズの系に対する数値計算も相補的に用いている。これまでに主としてオン・サイト相互作用のみを考慮したハバード模型に対する基底状態の補助場量子モンテカルロ計算、及び上記で述べたオフ・サイト相互作用までも考慮した拡張型ハバード模型に対する有限温度の補助場量子モンテカルロ計算を行っている。基底状態の計算は安定な数値計算が困難であるためオン・サイト相互作用に限定されているが、超伝導の対称性の競合を議論することができる。計算の結果、トリプレット超伝導においてはf波がp波よりも有利であること、またオフ・サイト相互作用を考慮しなくてもf波はd波に対してcompetitiveでありうることがわかった[Phys. Rev. B 69 (2004) 214511]。オフ・サイト相互作用を考慮した数値計算は現在のところ高温に限定されているため、超伝導対称性の議論にはいたっていないが、スピンと電荷の揺らぎ(感受率)に関しては計算することができる。その結果、2kFスピン揺らぎと2kF電荷揺らぎが同程度の大きさになるのはV’ + V⊥=U/2のときであることがわかり、乱雑位相近似の結果の正当性が裏付けられた[J. Phys. Soc. Jpn. 74 (2005) 1694-1697]。
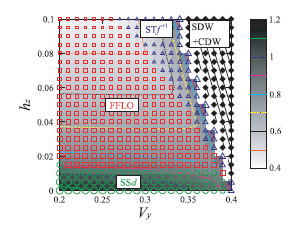
(TMTSF)2ClO4に対するいくつかの実験において、低磁場下ではスピン・シングレット、高磁場下ではスピン・トリプレット超伝導またはFulde-Ferrell-Larkin-Ovchinikov(FFLO)状態になっている可能性が指摘されている。我々はRPAの計算においてゼーマン効果を考慮し、スピン・トリプレットとシングレット超伝導の競合を調べた。その結果、2kFスピン揺らぎと2kF電荷揺らぎの共存によって生じるスピン・トリプレット超伝導機構に特有の効果により、磁場によってトリプレット超伝導が強く増強されることがわかった。このため、無磁場において、シングレット超伝導になっていたとしても、磁場下においてトリプレット超伝導に転移する可能性があることがわかった[Phys. Rev. B 77 (2008) 144513]。
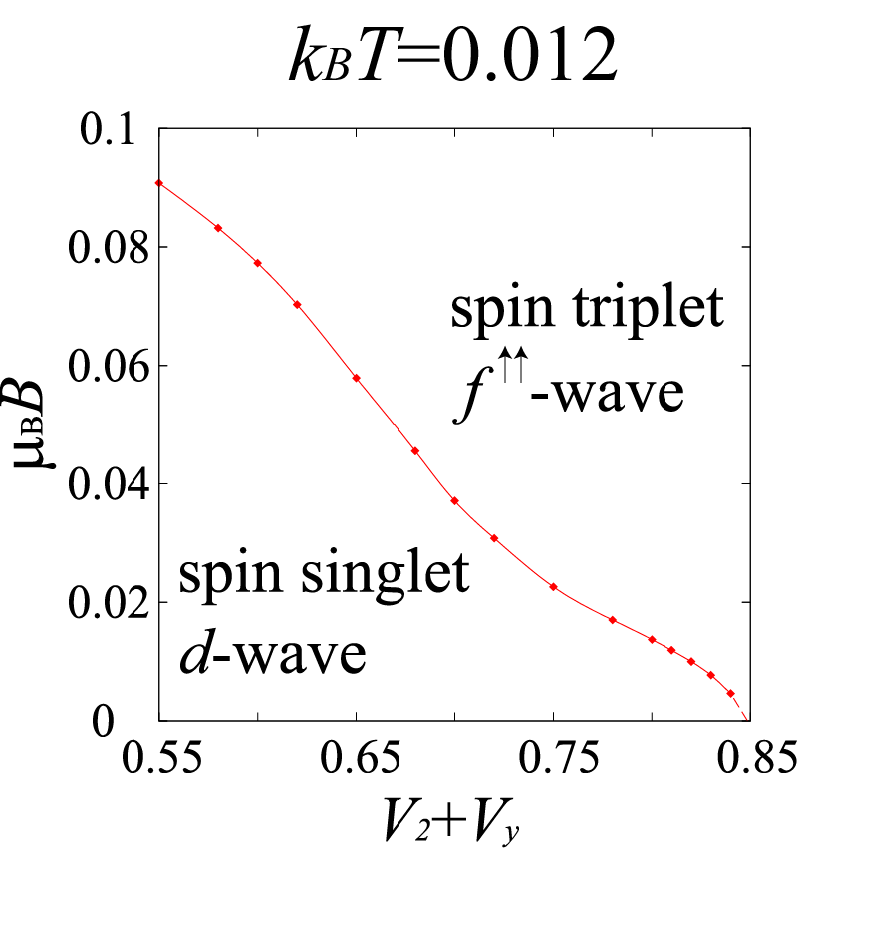
相澤・黒木は名大の横山・田仲らと共同研究を行い、TMTSF2XにおけるFFLO状態の可能性を微視的模型に基づいて研究した。これまで用いてきた、遠距離までの相互作用を取り込んだ微視的模型に対して、磁場の効果を取り込んだRPAを適用して、相図を得た。これまで、無磁場の状態でスピン・シングレット超伝導であっても、磁場をかけることによってスピン・トリプレット超伝導に転移する可能性があることを示してきたが、さらに、その間にFFLO状態が挟み込まれることがわかった。つまり、磁場をかけることによって、シングレットd波、FFLO、トリプレットf波と転移する可能性があることになる。さらに、このFFLO状態はシングレット成分とトリプレット成分が強く混合した状態であることも示した。この成果はPhysical Review Letter誌に掲載された[Phys. Rev. Lett. 102 (2009) 016403]。また、相澤はこの成果を含むTMTSF超伝導についての一連の研究を博士論文としてまとめ、平成21年3月に博士(理学)の学位を取得した。
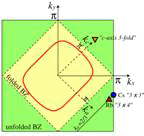
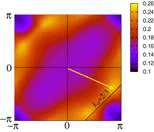
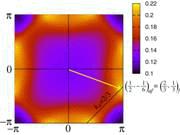
θ-(BEDT-TTF)2RbM’(SCN)4 (M’=Zn,Co)は低温でc軸方向に2倍周期を持つ電荷秩序を伴って絶縁体になるが、その転移温度TMIよりも高温の金属相においても、短距離電荷秩序的なものがあることが実験的に示唆される。特に、diffuse X-ray scatteringの実験では、(qa,qb,qc)=(2/3,k,1/4)にsatellite spotが観測される。また、θ-(BEDT-TTF)2CsM’(SCN)4においては、(2/3,k,1/3)と(0,0,1/2)短距離電荷秩序の共存が観測されている。ここで注目すべきことは、これらのa軸3倍周期の波数がRbM’,CsM’それぞれにおけるフェルミ面のネスティング・ベクトルQnestと一致しているということである(下図)。しかし、電子間相互作用としてU, Vc, Vpのみしか考えない場合、相互作用のフーリエ変換がQnestとは異なる位置にピークを持つため、相互作用とネスティングの効果が競合してしまい、Qnestとは異なる位置にRPA電荷感受率のピークがでてしまう。そこで、遠距離相互作用Va, Vq, V2cまでを考慮した結果、相互作用のフーリエ変換の絶対値がQnestを包含する広い領域で最大になり、その結果、Qnestの位置に電荷感受率のピークが得られることがわかった[J. Phys. Soc. Jpn. 75 (2006) 114716]。


有機超伝導体κ-(BEDT-TTF)2X (X=Cu(NCS)2等)は擬2次元的な有機超伝導体である。臨界温度は10Kを超えるものもあり、有機超伝導体の中では高い。結晶構造はBEDT-TTF分子がダイマーを組んでおり、ダイマーをひとつの固まりとみなすと、それが異方的三角格子を組んでいる。我々は異方的三角格子上のハバード模型を量子モンテカルロ法により扱い、銅酸化物と同様のd波超伝導相関が発達することを見た[Phys. Rev. B 60 (1999) 3060-3063]。しかし、その後の熱伝導やトンネルの実験においては、これとはギャップのノードの方向が45度回転した方向にある、という報告がなされた。そこで、我々はダイマーを一つの固まりとみなすのではなく、ダイマー内の分子一つ一つをサイトとみなすハバード模型をFLEX近似により、扱った。その結果、ダイマー化の度合いが現実的な領域では二種類のd波が拮抗し、アニオンの種類によってどちらの可能性もあり得ることがわかった[Phys. Rev. B 65 (2002) 100516(R) , J. Phys. Soc. Jpn. 75 (2006) 051013]。
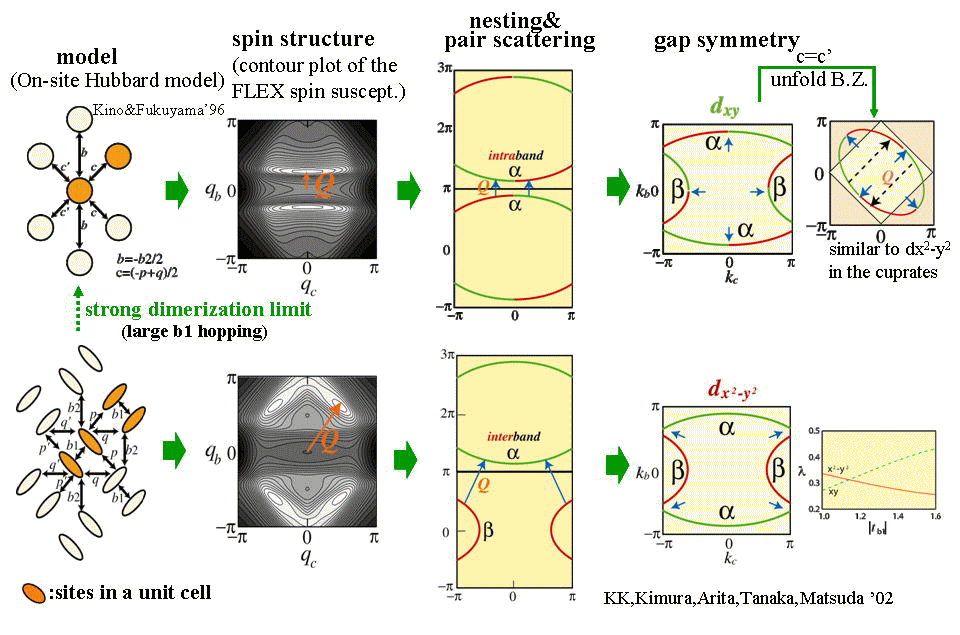
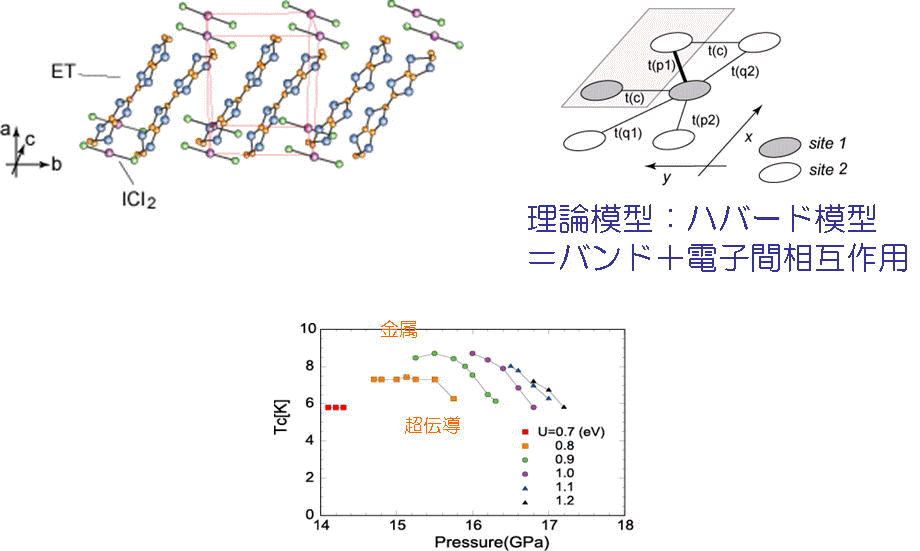
β’-(BEDT-TTF)2ICl2は常圧下では反強磁性的絶縁体であるが、高圧下において超伝導となり、そのTcは有機導体中最高である。我々はこの物質の圧力下における第一原理バンド構造を再現する2バンドのtight-binding模型(分子一個を一個のサイトとみなす模型)に対して、FLEX近似を適用し、超伝導の圧力相図を得た。超伝導が出る圧力領域が実験よりも高圧側に出るものの、かなりの精度で実験が再現できている[J. Phys. Soc. Jpn. 75 (2006) 034706]。
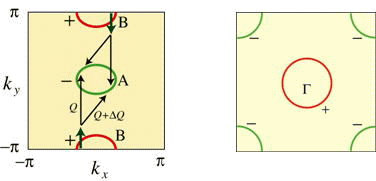
銅酸化物高温超伝導体の模型と考えられる2次元正方格子ハバード模型のhalf-filled近傍に対してFLEX近似を適用すると、ホッピング積分をtとして、0.03t程度のTcを持つd波超伝導が得られる。これは約100K程度に相当し、現実的な値である。同様の計算を3次元格子やdilute band fillingに対して行っても、これほど高い臨界温度は得られない[J. Phys. Soc. Jpn. 69 (2000) 1181-1191]。 その意味で、2次元正方格子のhalf-filling近傍は特異的であるといえ、このことは銅酸化物高温超伝導の臨界温度が特異的に高いことと関係があるように思える。一方で、もともとの電子系のエネルギーt(あるいはバンド幅8t)からみると、0.03tというTcは非常に低いように思える。斥力相互作用によって引き起こされるd波超伝導は、フォノンの低いエネルギースケールが律速にならないという意味で高い臨界温度を与えうる一方で、斥力相互作用を起源とするため、一般的には超伝導ギャップ関数にノード(節)が入ってしまい、フェルミ面上に完全にギャップが開かないことが超伝導のTcを下げる要因となりうる。我々はこの困難を回避する手段として、非連結フェルミ面による高温超伝導の可能性を提唱した。すなわち、図のように非連結なフェルミ面があり、その間にある程度のネスティングがあると、そのネスティングベクトル周辺にスピンの揺らぎが発生し、その揺らぎはフェルミ面間のペアリング相互作用(フェルミ面からフェルミ面へのペア散乱を引き起こす相互作用)を生み出す。スピン揺らぎによる相互作用は斥力的であるため、フェルミ面間で超伝導ギャップの符号は反転するが、フェルミ面が非連結であるため、フェルミ面上ではfull gapが開く。
このような状況が実現する具体例として、我々は図のような格子上の電子系を考案した[Phys. Rev. B 64 (2001) 024501, Phys. Rev. B 66 (2002) 132508, Phys. Rev. B 66 (2002) 184508]。FLEX近似による上記の計算と同様の計算を行うと、これらの系ではいずれも、最高で0.1t近いTcが得られることがわかった。
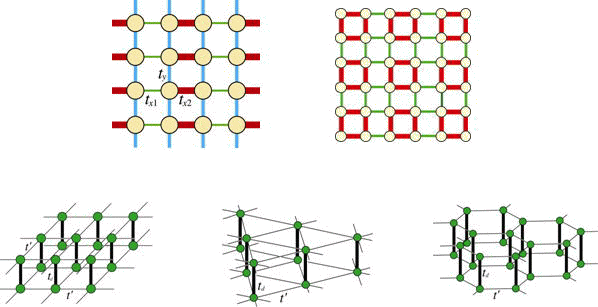
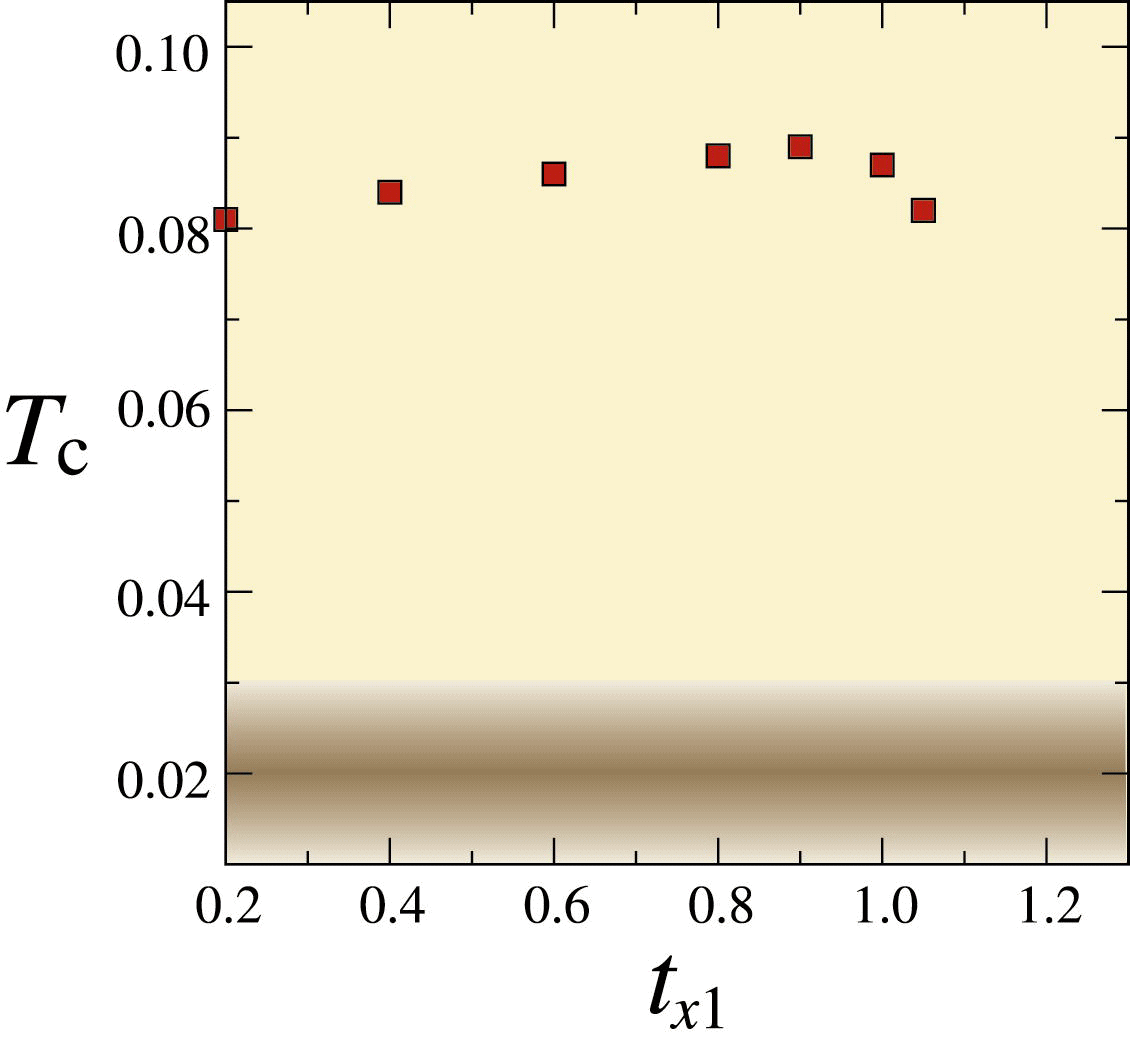
バンド幅の広いバンドと狭いバンドが共存し、フェルミ準位が狭いバンドの直上または直下にある場合を考える。バンド間の相互作用が強い場合、バンド間の電子対散乱を使うと、狭いバンドの高い状態密度のために広いバンド内に強いペアリング相互作用が生じる可能性がある。しかも広いバンド内にフェルミ準位があることは、有効質量を重くすることがないため、超伝導に有利である。このアイディアを具体的に実現するための例として、斜め方向のホッピング積分t'を考慮した梯子型格子を考えた。図のようにt'がないと、梯子系のバンドは2本の同一のバンドが上下にずれたものになるが、t'があると、一方のバンドは狭くなり、一方のバンドは広くなる。
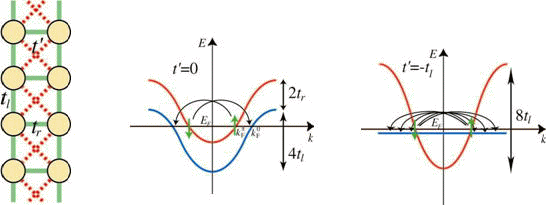
現実の梯子系として銅酸化物を考えた場合、FLEX近似によって得られるTcは図のようになった。ホールドープすると、フェルミ準位がnarrow band内にあるためにTcが高くならない(図の縦軸の0.01は40K程度)。これは現実のホールドープされた梯子系動産酸化物のTcが10Kのオーダーにとどまっていることと整合している。一方、電子ドープすると、フェルミ準位がnarrow bandの直上にくるため、Tcはホールドープ側よりも一桁高くなる[Phys. Rev. B 72 (2005) 212509]。
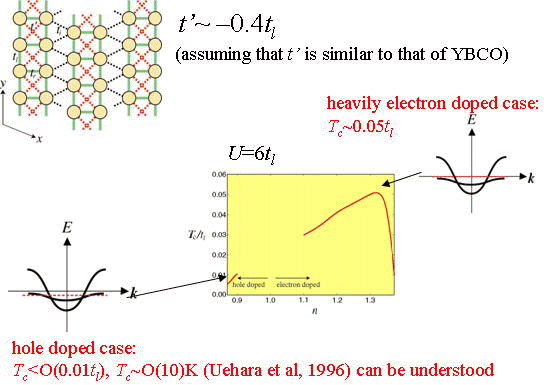
ハバード模型はサイト間の電子の移動(トランスファー積分)と電子間のオンサイト斥力のみを考慮する模型であり、このような単純な斥力模型において超伝導がおこるか、という問題は高温超伝導発見以前からも興味深い問題として調べられてきたが、特に数値計算の立場からは超伝導発現に否定的な結果が多く、ハバード模型で高温超伝導を説明することは難しい、という認識もあった。以下に述べる我々の研究成果はこの認識に再考を促すものといえる。
ハバード模型における超伝導の可能性を再考するきっかけとなったのは梯子型格子上のハバード模型、すなわちハバード梯子模型に関する研究である。2本鎖ハバード梯子においてはスピン・ギャップが開き、それに伴って超伝導相関が発達することが繰り込み群+ボゾン化の方法によりわかっている。一方、奇数本鎖の梯子系ではスピン・ギャップが開かないことがわかっているので、ナイーブには超伝導は起こらないと考えられる。我々は3本鎖ハバード梯子模型における超伝導の問題にボゾン化の方法により取組み、3つあるスピンの励起モードのうちの2つにギャップが開く(したがって全体としてはスピン・ギャップはない)ことに起因して、意外にも、超伝導相関が発達し得ることを示した[Phys. Rev. B 54 (1996) R9608-9611, J. Phys. Soc. Jpn. 67 (1998) 1377-1391]。
また、ボゾン化による上記の結果を有限系に対する数値計算で再現するには注意が必要であることを示した。それは、超伝導のエネルギー・スケールが有限系における準位の離散間隔よりも小さい可能性があるためである。実際、量子モンテカルロ法によってハバード梯子模型における超伝導相関を計算した結果、フェルミ準位近傍の準位の離散性が小さくなるようにトランスファー積分の値を選んだ場合にのみ、ボゾン化の結果と整合する超伝導相関の発達が得られることがわかった[Phys. Rev. B 54 (1996) R15641-15644, J. Phys. Soc. Jpn 66 (1997) 1599-1602, J. Phys. Soc. Jpn. 67 (1998) 1377-1391]。
我々はハバード梯子に関する上記の数値計算結果に鑑みて、従来、超伝導に否定的な数値計算結果が多かった二次元ハバード模型に立ち返った。そして梯子系の場合と同様にフェルミ準位近傍の準位の離散性に注意を払って量子モンテカルロ計算を行った結果、half-filled近傍においてdx2-y2波超伝導の相関関数が発達することを見いだした[Phys. Rev. B 56 (1997) R14287-14290]。